Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $MN$ với $M \in \left( O \right)$; $N \in \left( {O'} \right)$. Gọi $P$ là điểm đối xứng với $M$ qua $OO'$; $Q$ là điểm đối xứng với $N$ qua $OO'$.

$MN + PQ$ bằng

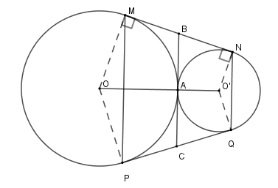
Kẻ tiếp tuyến chung tại $A$ của $\left( O \right);\left( {O'} \right)$ cắt $MN;PQ$ lần lượt tại $B;C$

Ta có $MNPQ$ là hình thang cân nên $\widehat {NMP} = \widehat {QPM}$.

 Tam giác $OMP$ cân tại $O$ nên $\widehat {OMP} = \widehat {OPM}$ suy ra $\widehat {OMP} + \widehat {PMN} = \widehat {OPM} + \widehat {MPQ} \Rightarrow \widehat {QPO} = 90^\circ $

$ \Rightarrow OP \bot PQ$ tại $P \in \left( O \right)$ nên $PQ$ là tiếp tuyến của $\left( O \right)$. Chứng minh tương tự ta có $PQ$ là tiếp tuyến của $\left( {O'} \right)$

Theo tính chất hai tiếp tuyến cắt nhau ta có

$BA = BM = BN;CP = CA = CQ$ suy ra $B;C$ lần lượt là trung điểm của $MN;PQ$ và $MN + PQ = 2MB + 2PC$

$= 2AB + 2AC = 2BC$

Lại có $BC$ là đường trung bình của hình thang $MNQP$ nên $MP + NQ = 2BC$

Do đó $MN + PQ = MP + NQ$.