Câu hỏi:
2 năm trước
Cho hai đường tròn $\left( {O;4cm} \right)$ và $\left( {O';3cm} \right)$ biết $OO' = 5cm$. Hai đường tròn trên cắt nhau tại $A$ và \(B\). Độ dài $AB$ là:
Trả lời bởi giáo viên
Đáp án đúng: b
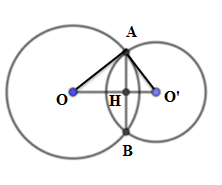
Xét tam giác $OAO'$ có $O{A^2} + O'{A^2} = OO{'^2}$ (vì ${4^2} + {3^2} = {5^2}$) nên tam giác $OAO'$ vuông tại $A$.
Xét tam giác $OAO'$ có $AH$ là đường cao nên $AH.OO' = OA.O'A \Rightarrow AH = \dfrac{{OA.O'A}}{{OO'}} = \dfrac{{4.3}}{5} = \dfrac{{12}}{5}$
Mà $AB = 2AH$ nên $AB = \dfrac{{24}}{5} = 4,8cm$
Hướng dẫn giải:
Dựa vào tính chất hai đường tròn cắt nhau.
Định lí Pi-ta-go đảo.
Hệ thức lượng trong tam giác vuông.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
