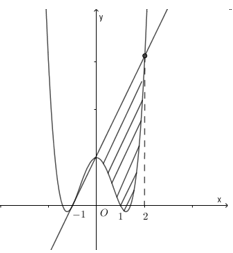
Cho (H) là hình phẳng giới hạn bởi các đồ thị hàm số \(y=e,\,\,y={{e}^{x}}\) và \(y=(1-e)x+1\) (tham khảo hình vẽ bên). Diện tích của (H) là
Trả lời bởi giáo viên
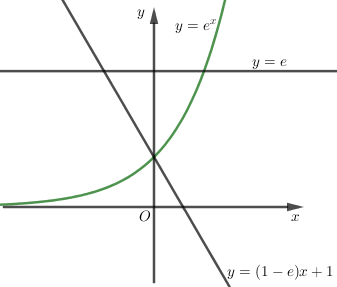
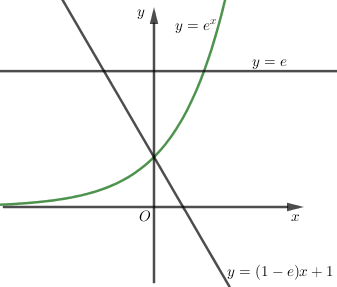
Tọa độ giao điểm của \(y=e\) và \(y=(1-e)x+1\) là \(A(-1;e)\)
Tọa độ giao điểm của \(y=(1-e)x+1\) và \(y={{e}^{x}}\) là \(B(0;1)\)
Tọa độ giao điểm của \(y=e\) và \(y={{e}^{x}}\) là \(C(1;e)\)
Diện tích hình (H):
\(\begin{align} S=\int\limits_{-1}^{0}{\left| e-\left( (1-e)x+1 \right) \right|}dx+\int\limits_{0}^{1}{\left| e-{{e}^{x}} \right|dx}=\int\limits_{-1}^{0}{\left( e-\left( (1-e)x+1 \right) \right)}dx+\int\limits_{0}^{1}{\left( e-{{e}^{x}} \right)dx} \\ =\int\limits_{-1}^{0}{\left( e-1-(1-e)x \right)}dx+\int\limits_{0}^{1}{\left( e-{{e}^{x}} \right)dx}=\left( e-1 \right)\left. \left( x+\frac{1}{2}{{x}^{2}} \right) \right|_{-1}^{0}+\left. \left( e\,x-{{e}^{x}} \right) \right|_{0}^{1} \\ =\left( e-1 \right)\left( 0+1-\frac{1}{2} \right)+\left( e-e-0+1 \right)=\frac{1}{2}e+\frac{1}{2}=\frac{e+1}{2} \\ \end{align}\)
Hướng dẫn giải:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số \(y=f(x),\,\,y=g(x)\), trục hoành và hai đường thẳng \(x=a;\,\,x=b\) được tính theo công thức : \(S=\int\limits_{a}^{b}{\left| f(x)-g(x) \right|dx}\)