Câu hỏi:
2 năm trước
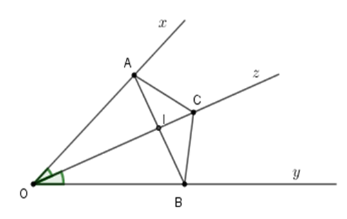
Cho góc nhọn $xOy$ và $Oz$ là tia phân giác của góc đó. Trên tia $Ox$ lấy điểm $A$ và trên tia $Oy$ lấy điểm $B$ sao cho $OA = OB.$ Gọi $C$ là một điểm bất kỳ trên tia $Oz.$
Gọi \(I\) là giao của \(AB\) và \(Oz.\) Tính góc \(AIC.\)
Trả lời bởi giáo viên
Đáp án đúng: b
Xét tam giác \(AOI\) và \(BOI\) có
+ \(OA = OB\left( {gt} \right)\)
+ \(\widehat {AOI} = \widehat {BOI}\) (tính chất tia phân giác)
+ Cạnh $OI$ chung
Suy ra \(\Delta AOI = \Delta BOI\left( {c - g - c} \right)\)
Do đó \(\widehat {AIO} = \widehat {BIO}\) (hai góc tương ứng) mà \(\widehat {AIO} + \widehat {BIO} = 180^\circ \) nên \(\widehat {AIO} = \widehat {BIO} = \dfrac{{180^\circ }}{2} = 90^\circ \)
Hay \(OC \bot AB \Rightarrow \widehat {AIC} = 90^\circ .\)
Hướng dẫn giải:
Sử dụng trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
