Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right)\), lấy điểm \(M\) nằm ngoài \(\left( O \right)\) sao cho \(OM = 2R.\) Từ M kẻ tiếp tuyến \(MA\) và \(MB\) với \(\left( O \right)\) (\(A,B\) là các tiếp điểm).
Số đo cung \(AB\) nhỏ là
Trả lời bởi giáo viên
Đáp án đúng: b
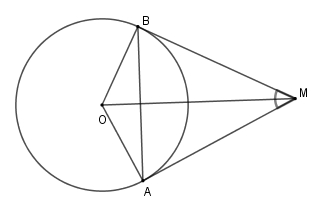
Xét đường tròn $\left( O \right)$ có $MA;MB$ là hai tiếp tuyến cắt nhau tại $M$ nên $OM$ là tia phân giác của góc $\widehat {AOB}$
Suy ra $\widehat {AOB} = 2\widehat {AOM} = 2.60^\circ = 120^\circ $ mà $\widehat {AOB}$ là góc ở tâm chắn cung \(AB\)
Nên số đo cung nhỏ \(AB\) là $120^\circ $.
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau và số đo cung

