Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right)\), lấy điểm \(M\) nằm ngoài \(\left( O \right)\) sao cho \(OM = 2R.\) Từ M kẻ tiếp tuyến \(MA\) và \(MB\) với \(\left( O \right)\) (\(A,B\) là các tiếp điểm).
Số đo góc $\widehat {AOM}$ là
Trả lời bởi giáo viên
Đáp án đúng: d
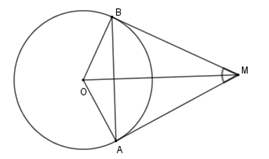
Xét tam giác $AOM$ vuông tại $A$ ta có $\cos \widehat {AOM} = \dfrac{{OA}}{{OM}} = \dfrac{R}{{2R}} = \dfrac{1}{2} \Rightarrow \widehat {AOM} = 60^\circ .$
Hướng dẫn giải:
Sử dụng tỉ số lượng giác của góc nhọn

