Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là trung điểm của bán kính \(OA\). Dây \(CD\) vuông góc với \(OA\) tại $H$ . Tính số đo cung lớn \(CD.\)
Trả lời bởi giáo viên
Đáp án đúng: c
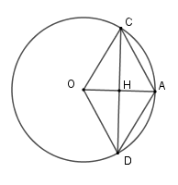
Xét đường tròn$\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD$
Tứ giác $OCAD$ có hai đường chéo vuông góc và giao nhau tại trung điểm mỗi đường nên $OCAD$ là hình thoi.
$ \Rightarrow OC = CA$ mà $OC = OA$ nên $OC = OA = AC$ hay tam giác $OAC$ đều $ \Rightarrow \widehat {COA} = 60^\circ \Rightarrow \widehat {COD} = 120^\circ $
Do đó số đo cung nhỏ $CD$ là $120^\circ $ và số đo cung lớn $CD$ là $360^\circ - 120^\circ = 240^\circ $.
Hướng dẫn giải:
+) Sử dụng liên hệ giữa đường kính và dây
+) Kiến thức về số đo cung

