Cho đường tròn (O; R) đường kính AB. Vẽ các tia tiếp tuyến Ax, By với nửa đường tròn. Lấy điểm M di động trên tía Ax, điểm N di động trên tia Oy sao cho \(AM.BN = {R^2}.\)
Chọn câu đúng:
Trả lời bởi giáo viên
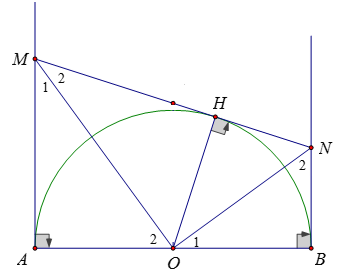
Vẽ \(OH \bot MN,{\rm{ }}H \in MN.\;\) Vì \(AM.BN = {R^2}\; = AO.BO\) nên \(\dfrac{{AM}}{{BO}} = \dfrac{{AO}}{{BN}}\)
Xét ΔAOM và ΔBNO có: \(\widehat {MAO} = \widehat {NBO} = 90^\circ ;\,\dfrac{{AM}}{{BO}} = \dfrac{{AO}}{{BN}}\) \( \Rightarrow \Delta AOM\backsim\Delta BNO{\rm{ }}\left( {c.g.c} \right)\) \( \Rightarrow \widehat {{M_1}} = \widehat {{O_1}};\,\widehat {{O_2}} = \widehat {{N_2}}\)
Do đó góc MON bằng \({90^0}\)
Ta có: \(\dfrac{{AM}}{{BO}} = \dfrac{{OM}}{{ON}} \) (do \(\Delta AOM\backsim\Delta BNO\)) \(\Rightarrow \dfrac{{AM}}{{OM}} = \dfrac{{OA}}{{ON}}\)
Do đó \(\Delta AOM\backsim\Delta ONM{\rm{ }}\left( {c.g.c} \right)\) \( \Rightarrow \widehat {{M_1}} = \widehat {{M_2}}\)
\( ΔAOM = ΔHOM\) (cạnh huyền, góc nhọn)
\( \Rightarrow AO = OH \Rightarrow OH = R,\) do đó MN là tiếp tuyến của đường tròn (O)
Hướng dẫn giải:
Sử dụng tam giác đồng dạng, tam giác bằng nhau để chứng minh \(OH = R.\)


