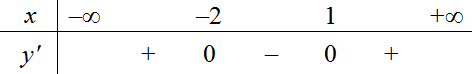Cho đồ thị hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + \dfrac{1}{3}x + c\) (\(a\), \(b\), \(c \in \mathbb{R}\)) và đường thẳng \(y = g\left( x \right)\) có đồ thị như hình vẽ:

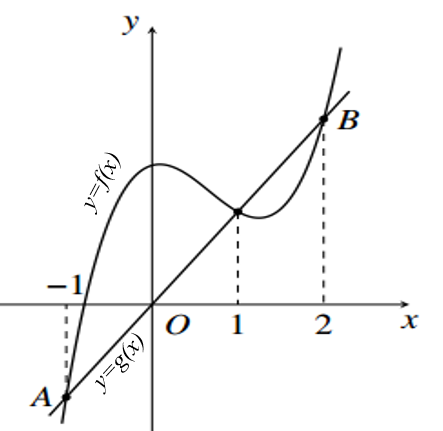
Biết \(AB = 5\), diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) bằng

Gọi \(g\left( x \right) = mx\) \(\left( {m > 0} \right)\). Ta có \(A\left( { - 1\,;\, - m} \right)\,\); \(B\left( {2\,;\,2m} \right)\).

Khi đó \(AB = \sqrt {9 + 9{m^2}}  = 5 \Leftrightarrow m = \dfrac{4}{3}\).

Phương trình hoành độ giao điểm: \(f\left( x \right) = g\left( x \right) \Leftrightarrow a{x^3} + b{x^2} - x + c = 0\).

Mặt khác \(a{x^3} + b{x^2} - x + c = a\left( {{x^2} - 1} \right)\left( {x - 2} \right)\)\( \Leftrightarrow a{x^3} + b{x^2} - x + c = a{x^3} - 2a{x^2} - ax + 2a\).

Đồng nhất hệ số ta đươc \(a = 1\), \(b =  - 2\), \(c = 2\). Vậy \(y = f\left( x \right) = {x^3} - 2{x^2} + \dfrac{1}{3}x + 2\).

Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) là \(S = \int\limits_1^2 {\left( {{x^3} - 2{x^2} + \dfrac{1}{3}x + 2} \right){\rm{d}}x}  = \dfrac{{19}}{{12}}.\)