Cho \(\Delta ABC\) vuông tại $A,$ đường cao $AH.$ Gọi $I$ và $K$ lần lượt là hình chiếu của $H$ lên $AB$ và $AC.$ Tam giác \(AIK\) đồng dạng với tam giác nào dưới đây?

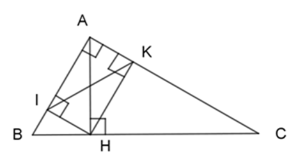
+) Có I, K lần lượt là hình chiếu của H lên AB và AC.

\( \Rightarrow \widehat {HIA} = \widehat {HKA} = {90^0}\)

Xét tứ giác AIHK có:

\(\widehat {IAK} = \widehat {HIA} = \widehat {HKA} = {90^0}\)

\( \Rightarrow \) Tứ giác AIHK là hình chữ nhật. (dhnb)

+) Xét \(\Delta AIK\) và \(\Delta IAH\) ta có:

\(AI\;chung\)

\(AK = IH\)(theo tính chất của hình chữ nhật)

\(AH = IK\;\) (theo tính chất của hình chữ nhật)

\( \Rightarrow \Delta AIK = \Delta IAH\;(c - c - c)\) (1)

Xét 2 tam giác vuông \(\Delta IAH\) và \(\Delta HAB\) có: \(\widehat A\) chung

\( \Rightarrow \Delta IAH \backsim \Delta HAB\;(g - g)\) (2)

Xét 2 tam giác vuông \(\Delta HAB\) và \(\Delta ACB\) có: \(\widehat B\) chung

\( \Rightarrow \)\(\Delta HAB \backsim \Delta ACB\;\;\left( {g - g} \right)\) (3)

Từ (1), (2) và (3) ta có: \(\Delta AIK \backsim \Delta ACB\)