Câu hỏi:
2 năm trước
Cho $\Delta ABC$ cân tại $A,$ lấy $M$ là trung điểm của $BC$. Kẻ $MH \bot AB{\rm{ }}(H \in AB),{\rm{ }}MK \bot AC{\rm{ }}(K \in AC).$ Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: d
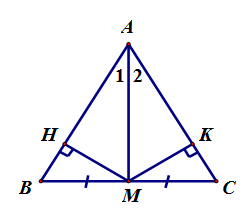
+) Xét $\Delta AMB$ và $\Delta AMC$ có:
$AB = AC$ ($\Delta ABC$ cân tại $A$ )
$AM$ chung
$MB = MC$ ($M$ là trung điểm $BC$ )
Suy ra $\Delta AMB{\rm{ }} = {\rm{ }}\Delta AMC$ (cạnh – cạnh – cạnh)
+) Ta có: ∆AMB = ∆AMC (cmt)
\( \Rightarrow \widehat {AMB} = \widehat {AMC}\) ( hai góc tương ứng)
Mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) ( hai góc kề bù)\( \Rightarrow \widehat {AMB} = \widehat {AMC} = 180^\circ :2 = 90^\circ \)
Suy ra AM $ \bot $ BC.
+) Xét ∆HMB và ∆KMC có
\(\widehat {BHM} = \widehat {CKM} = 90^\circ \) (gt)
MB = MC (M là trung điểm của BC)
$\widehat {HBM} = \widehat {KCM}$ (tam giác ABC cân tại A)
Suy ra ∆HMB = ∆KMC (cạnh huyền-góc nhọn), suy ra MH = MK (hai cạnh tương ứng).
Hướng dẫn giải:
+) Sử dụng trường hợp bằng nhau cạnh – cạnh – cạnh của tam giác, trường hợp bằng nhau cạnh huyền-góc nhọn của tam giác vuông để chứng minh các tam giác bằng nhau
+) Sử dụng tính chất hai tam giác bằng nhau, tính chất hai góc kề bù
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
