Câu hỏi:

2 năm trước

Cho các số phức z thỏa mãn |z|= 2 và điểm A trong hình vẽ là điểm biểu diễn của z. Biết rằng trong hình vẽ, điểm biểu diễn số phức $w = \dfrac{{ - 4}}{z}$ là một trong bốn điểm M, N, P, Q
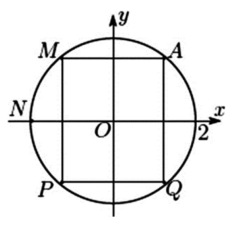
Khi đó điểm biểu diễn của số phức w là

Điểm N

Điểm Q

Điểm P

Điểm M

Xem đáp án

116 lượt xem

Đề thi tư duy định lượng - Đề số 8 - Tư duy định lượng - Đánh Giá Năng Lực. Thi ngay

Trả lời bởi giáo viên

Đáp án đúng: d

Đặt $z = x + yi$ $= > {x^2} + {y^2} = 4 = > A\left( {x;y} \right)$

Xét $w = \dfrac{{ - 4}}{z} = \dfrac{{ - \left( {{x^2} + {y^2}} \right)}}{{x + yi}}$ $= \dfrac{{ - \left( {x+yi} \right)\left( {x - yi} \right)}}{{\left( {x + yi} \right)}} = - x + yi$

Điểm biểu diễn số phức w đối xứng A qua Oy

=> Điểm M.

Hướng dẫn giải:

- Đặt $z = x + yi$

- Sử dụng công thức $\left| z \right| = \sqrt {{x^2} + {y^2}}$

- Công thức: $(x+yi)(x-yi)=z.\overline{z}=|z|^2=x^2+y^2$

- Biểu diễn w theo x và y.

Câu hỏi khác

Câu 1:

Hai tháng đầu năm 2020, lượng khách Quốc tế đến Việt Nam đạt 3,24 triệu lượt người, tăng 4,8% so với cùng kỳ năm trước, đây là mức tăng thấp nhất kể từ năm 2016.

Dựa vào dữ liệu ở trên hãy cho biết so với cùng kỳ năm trước thì lượng khách quốc tế qua 2 tháng đầu năm

2019 tăng bao nhiêu phần trăm?

8,04%

4,8%

13,28%

15%

Xem đáp án

132

132 lượt xem
Xem đáp án
2 năm trước

Câu 2:

Tìm các giá trị của tham số $m$ để phương trình ${x^2} - 2\left( {m + 1} \right)x + 1 = 0$ có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng $\left( {0;\,\,1} \right)$ .

$m > 0$

$m < 0$

$m = 0$

Không xác định được

Xem đáp án

130

130 lượt xem
Xem đáp án
2 năm trước

Câu 3:

Cho hình lăng trụ đứng $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông, $AB = BC = a,$ $A'B = a\sqrt 3$ . Gọi $M$ là trung điểm của cạnh $BC.$ Tính khoảng cách giữa hai đường thẳng $AM$ và $B’C.$

$d = \dfrac{{a\sqrt {42} }}{7}.$

$d = \dfrac{{a\sqrt {21} }}{7}.$

$d = \dfrac{{a\sqrt {14} }}{7}.$

$d = \dfrac{{a\sqrt 7 }}{7}.$

Xem đáp án

124

124 lượt xem
Xem đáp án
2 năm trước

Câu 4:

Hệ phương trình $\left\{ {\begin{array}{*{20}{c}}{x.y + x + y = 11}\\{{x^2}y + x{y^2} = 30}\end{array}} \right.$

có 2 nghiệm $\left( {2;3} \right)$ và $\left( {1;5} \right)$ .

có 2 nghiệm $\left( {2;1} \right)$ và $\left( {3;5} \right)$ .

có 1 nghiệm là $\left( {5;6} \right).$

có 4 nghiệm $\left( {2;3} \right),\left( {3;2} \right),\left( {1;5} \right),\left( {5;1} \right).$

Xem đáp án

127

127 lượt xem
Xem đáp án
2 năm trước

Câu 5:

Tập nghiệm $S$ của hệ bất phương trình $\left\{ \begin{array}{l}2x - 1 < - x + 2017\\3 + 3x > \dfrac{{2018 - 2x}}{2}\end{array} \right.$ là:

$S = \emptyset .$

$S = \left( {\dfrac{{2012}}{8};\dfrac{{2018}}{3}} \right).$

$S = \left( { - \infty ;\dfrac{{2012}}{8}} \right).$

$S = \left( {\dfrac{{2018}}{3}; + \infty } \right).$

Xem đáp án

112

112 lượt xem
Xem đáp án
2 năm trước

Câu 6:

Cho đường thẳng $d$ có ptts: $\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 + t\end{array} \right.;t \in R$ . Tìm điểm $M \in d$ sao cho khoảng cách từ $M$ đến điểm $A(0;1)$ một khoảng bằng $5.$

$M\left( { - 4;4} \right)$ hoặc $M\left( {\dfrac{{ - 24}}{5};\dfrac{{ - 2}}{5}} \right)$

$M\left( {\dfrac{{ - 24}}{5};\dfrac{{ - 2}}{5}} \right)$

$M\left( { - 4;4} \right)$

$M\left( {4;4} \right)$ hoặc $M\left( {\dfrac{{ - 24}}{5};\dfrac{{ - 2}}{5}} \right)$

Xem đáp án

120

120 lượt xem
Xem đáp án
2 năm trước

Câu 7:

Tìm tất cả các giá trị của tham số $m$ để phương trình ${x^2} + {y^2} + 2mx - 4\left( {m + 1} \right)y + 4{m^2} + 5m + 2 = 0$ là phương trình của một đường tròn trong mặt phẳng tọa độ $Oxy$ .

$- 2 < m < - 1$

$\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.$

$\left[ \begin{array}{l}m < - 2\\m > - 1\end{array} \right.$

$\left[ \begin{array}{l}m \le - 2\\m \ge - 1\end{array} \right.$

Xem đáp án

113

113 lượt xem
Xem đáp án
2 năm trước

Cho các số phức z thỏa mãn |z|= 2 và điểm A trong hình vẽ là điểm biểu diễn của z. Biết rằng trong hình vẽ, điểm biểu diễn số phức $w = \dfrac{{ - 4}}{z}$ là một trong bốn điểm M, N, P, Q
Khi đó điểm biểu diễn của số phức w là

Trả lời bởi giáo viên

Câu hỏi khác

Tìm các giá trị của tham số $m$ để phương trình ${x^2} - 2\left( {m + 1} \right)x + 1 = 0$ có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng $\left( {0;\,\,1} \right)$ .

Cho hình lăng trụ đứng $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông, $AB = BC = a,$ $A'B = a\sqrt 3$ . Gọi $M$ là trung điểm của cạnh $BC.$ Tính khoảng cách giữa hai đường thẳng $AM$ và $B’C.$

Hệ phương trình $\left\{ {\begin{array}{*{20}{c}}{x.y + x + y = 11}\\{{x^2}y + x{y^2} = 30}\end{array}} \right.$

Tập nghiệm $S$ của hệ bất phương trình $\left\{ \begin{array}{l}2x - 1 < - x + 2017\\3 + 3x > \dfrac{{2018 - 2x}}{2}\end{array} \right.$ là:

Cho đường thẳng $d$ có ptts: $\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 + t\end{array} \right.;t \in R$ . Tìm điểm $M \in d$ sao cho khoảng cách từ $M$ đến điểm $A(0;1)$ một khoảng bằng $5.$

Tìm tất cả các giá trị của tham số $m$ để phương trình ${x^2} + {y^2} + 2mx - 4\left( {m + 1} \right)y + 4{m^2} + 5m + 2 = 0$ là phương trình của một đường tròn trong mặt phẳng tọa độ $Oxy$ .

Đề thi - đề kiểm tra Xem thêm

Chúng tôi

Học tốt

Liên kết

Mạng xã hội

Cho các số phức z thỏa mãn |z|= 2 và điểm A trong hình vẽ là điểm biểu diễn của z. Biết rằng trong hình vẽ, điểm biểu diễn số phức w=−4zw = \dfrac{{ - 4}}{z} là một trong bốn điểm M, N, P, QKhi đó điểm biểu diễn của số phức w là

Trả lời bởi giáo viên

Câu hỏi khác

Tìm các giá trị của tham số mm để phương trình x2−2(m+1)x+1=0{x^2} - 2\left( {m + 1} \right)x + 1 = 0 có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0;1)\left( {0;\,\,1} \right).

Cho hình lăng trụ đứng ABC.A′B′C′ABC.A’B’C’ có đáy ABCABC là tam giác vuông, AB=BC=a,AB = BC = a, A′B=a√3A'B = a\sqrt 3 . Gọi MM là trung điểm của cạnh BC.BC. Tính khoảng cách giữa hai đường thẳng AMAM và B′C.B’C.

Hệ phương trình {x.y+x+y=11x2y+xy2=30\left\{ {\begin{array}{*{20}{c}}{x.y + x + y = 11}\\{{x^2}y + x{y^2} = 30}\end{array}} \right.

Tập nghiệm SS của hệ bất phương trình {2x−1<−x+20173+3x>2018−2x2\left\{ \begin{array}{l}2x - 1 < - x + 2017\\3 + 3x > \dfrac{{2018 - 2x}}{2}\end{array} \right. là:

Cho đường thẳng dd có ptts: {x=2+2ty=3+t;t∈R\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 + t\end{array} \right.;t \in R. Tìm điểm M∈dM \in d sao cho khoảng cách từ MM đến điểm A(0;1)A(0;1) một khoảng bằng 5.5.

Tìm tất cả các giá trị của tham số mm để phương trình x2+y2+2mx−4(m+1)y+4m2+5m+2=0{x^2} + {y^2} + 2mx - 4\left( {m + 1} \right)y + 4{m^2} + 5m + 2 = 0 là phương trình của một đường tròn trong mặt phẳng tọa độ OxyOxy.

Đề thi - đề kiểm tra Xem thêm

Cho các số phức z thỏa mãn |z|= 2 và điểm A trong hình vẽ là điểm biểu diễn của z. Biết rằng trong hình vẽ, điểm biểu diễn số phức $w = \dfrac{{ - 4}}{z}$ là một trong bốn điểm M, N, P, Q
Khi đó điểm biểu diễn của số phức w là

Tìm các giá trị của tham số $m$ để phương trình ${x^2} - 2\left( {m + 1} \right)x + 1 = 0$ có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng $\left( {0;\,\,1} \right)$ .

Cho hình lăng trụ đứng $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông, $AB = BC = a,$ $A'B = a\sqrt 3$ . Gọi $M$ là trung điểm của cạnh $BC.$ Tính khoảng cách giữa hai đường thẳng $AM$ và $B’C.$

Hệ phương trình $\left\{ {\begin{array}{*{20}{c}}{x.y + x + y = 11}\\{{x^2}y + x{y^2} = 30}\end{array}} \right.$

Tập nghiệm $S$ của hệ bất phương trình $\left\{ \begin{array}{l}2x - 1 < - x + 2017\\3 + 3x > \dfrac{{2018 - 2x}}{2}\end{array} \right.$ là:

Cho đường thẳng $d$ có ptts: $\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 + t\end{array} \right.;t \in R$ . Tìm điểm $M \in d$ sao cho khoảng cách từ $M$ đến điểm $A(0;1)$ một khoảng bằng $5.$

Tìm tất cả các giá trị của tham số $m$ để phương trình ${x^2} + {y^2} + 2mx - 4\left( {m + 1} \right)y + 4{m^2} + 5m + 2 = 0$ là phương trình của một đường tròn trong mặt phẳng tọa độ $Oxy$ .