Câu hỏi:
2 năm trước
Cho biểu thức \(C = \dfrac{{12}}{{3n - 2}}\). Tìm tất cả các giá trị nguyên của \(n\) để giá trị của \(C\) là một số tự nhiên.
Trả lời bởi giáo viên
Đáp án đúng: b
Vì \(C \in N\) nên \(C \in Z.\) Do đó ta tìm \(n \in Z\) để \(C \in Z\)
Vì \(n \in Z\) nên để \(C \in Z\) thì \(3n - 2 \in U\left( {12} \right) = \left\{ { \pm 1; \pm 2; \pm 3; \pm 4; \pm 6; \pm 12} \right\}\)
Ta có bảng:
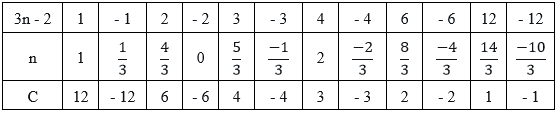
Vì \(C \in N\) và \(n \in Z\) nên ta chỉ nhận các giá trị \(n = 1;n = 2\).
Hướng dẫn giải:
- \(C\) là số tự nhiên suy ra \(C\) là số nguyên hay \(3n - 2\) là ước của \(12\)
- Từ đó tìm các giá trị của \(n\) rồi thử lại kiểm tra lại điều kiện \(C\) là số tự nhiên.
Câu hỏi khác
- Bài tập các dạng toán về mở rộng khái niệm phân số. phân số bằng nhau môn toán 6 sách KNTT có lời giải
- Bài tập tính chất cơ bản của phân số môn toán 6 sách KNTT có lời giải
- Bài tập so sánh phân số môn toán 6 sách KNTT có lời giải
- Bài tập các dạng toán về tính chất cơ bản của phân số môn toán 6 sách KNTT có lời giải
- Bài tập mở rộng phân số. phân số bằng nhau môn toán 6 sách KNTT có lời giải
