Cho ba hình cầu có bán kính lần lượt là \({R_1},{R_2},{R_3}\) đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ dài cạnh lần lượt là 2, 3, 4. Tính tổng \({R_1} + {R_2} + {R_3}\):
Trả lời bởi giáo viên
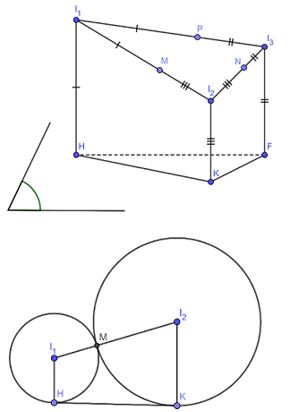
Gọi \({I_1},{I_2},{I_3}\) là tâm của các hình cầu, \(M,N,P\) là các tiếp điểm của các hình cầu (như hình vẽ), \(H,K,F\) là tiếp ba hình cầu với mặt phẳng (P) (như hình vẽ).
Xét mặt phẳng \(\left( {{I_1}{I_2}KH} \right)\), có:
\(\begin{array}{l}HK = \sqrt {{I_1}{I_2}^2 - {{\left( {{I_2}K - {I_1}H} \right)}^2}} \,\\\,\,\,\,\,\,\,\,\, = \sqrt {{{\left( {{R_1} + {R_2}} \right)}^2} - {{\left( {{R_1} - {R_2}} \right)}^2}} \\\,\,\,\,\,\,\,\, = \sqrt {4{R_1}{R_2}} = 2 \Rightarrow {R_1}{R_2} = 1\end{array}\)
Tương tự, \({R_1}{R_3} = \dfrac{9}{4},\,{R_2}{R_3} = 4\)
\( \Rightarrow {R_1}{R_2}{R_3} = \sqrt {1.\dfrac{9}{4}.4} = 3 \Rightarrow \left\{ \begin{array}{l}{R_1} = \dfrac{3}{4}\\{R_2} = \dfrac{4}{3}\\{R_3} = 3\end{array} \right.\).
Vậy \({R_1} + {R_2} + {R_3} = \dfrac{3}{4} + \dfrac{4}{3} + 3 = \dfrac{{61}}{{12}}\).