Cho \(\widehat {AOB} = {135^0}\) . Vẽ \(\widehat {BOC}\)  và \(\widehat {AO{\rm{D}}}\) kề bù với \(\widehat {AOB}\) .Chọn câu đúng nhất.

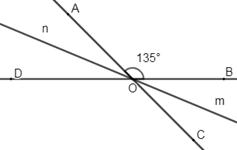
+ Các tia $OA$ và $OC,{\rm{ }}OB$ và $OD$ là các tia đối nhau, do đó hai góc \(\widehat {BOC}\) và \(\widehat {AO{\rm{D}}}\) là hai góc đối đỉnh nên A đúng.

Ta có: $\widehat {AOB} + \widehat {BOC} = {180^0}$ (kề bù) $ \Rightarrow \widehat {BOC} = {180^0} - \widehat {AOB} = {180^0} - {135^0} = {45^0}$  nên B đúng.

+ Gọi $Om,{\rm{ }}On$ lần lượt là hai tia phân giác của \(\widehat {BOC}\) và \(\widehat {AO{\rm{D}}}\).

Do đó, ta có: \(\widehat {BOm} = \widehat {mOC} = \dfrac{{\widehat {BOC}}}{2},\,\widehat {AOn} = \widehat {DOn} = \dfrac{{\widehat {AOD}}}{2}\) (tính chất tia phân giác của 1 góc)

\(\widehat {BOC} = \widehat {AO{\rm{D}}}\) (đối đỉnh) \( \Rightarrow \widehat {BOm} = \widehat {mOC} = \widehat {DOn} = \widehat {nOA}\)

\( \Rightarrow \widehat {nOm} = \widehat {nO{\rm{D}}} + \widehat {DOC} + \widehat {COm} \)\(= \widehat {nO{\rm{D}}} + \widehat {nOA} + \widehat {DOC} = \widehat {AO{\rm{D}}} + \widehat {DOC} = {180^0}\) (kề bù)

\( \Rightarrow \widehat {nOm}\) là góc bẹt, vì thế hai tia $Om$ và $On$ là hai tia đối nhau.

Vậy hai tia phân giác của hai góc đối đỉnh là hai tia đối nhau nên  C đúng.