Câu hỏi:
3 năm trước
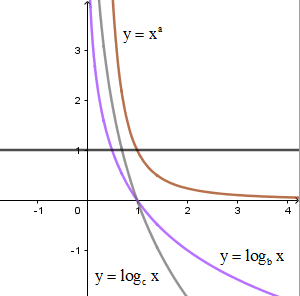
Cho \(a\) là số thực tùy ý và \(b,c\) là các số thực dương khác \(1\). Hình vẽ bên là đồ thị của ba hàm số \(y = {\log _b}x;y = {\log _c}x;y = {x^a}\left( {x > 0} \right)\). Khẳng định nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: b
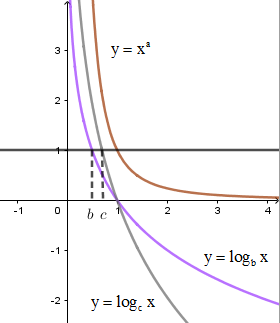
Ta thấy hàm số \(y = {x^a}\) nghịch biến nên \(a < 0\) nên loại C, D.
Kẻ đường thẳng \(y = 1\) cắt hai đồ thị hàm số \(y = {\log _b}x;y = {\log _c}x\) tại hai điểm lần lượt có hoành độ \(x = b;x = c\). Quan sát đồ thị ta thấy \(b < c\).
Vậy \(a < b < c\).
Hướng dẫn giải:
Quan sát các đồ thị hàm số và nhận xét.
Giải thích thêm:
HS sẽ nhầm lẫn ở việc nhận dạng: Nhiều em sẽ nhận xét đồ thị hàm số \(y = {x^a}\) nằm ở phía trên cả hai đồ thị hàm số \(y = {\log _b}x;y = {\log _c}x\) nên kết luận ngay \(a > b,c\) nên chọn sai đáp án.

