Câu hỏi:
2 năm trước
Cho $2$ đường thẳng: $d:y = x + 3;d':y = \dfrac{{ - 2}}{3}x + \dfrac{4}{3}$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $C$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành; $B$ và $D$ lần lượt là giao điểm của $d$ và $d'$ với trục tung. Khi đó diện tích tam giác $CMB$ là:
Trả lời bởi giáo viên
Đáp án đúng: b
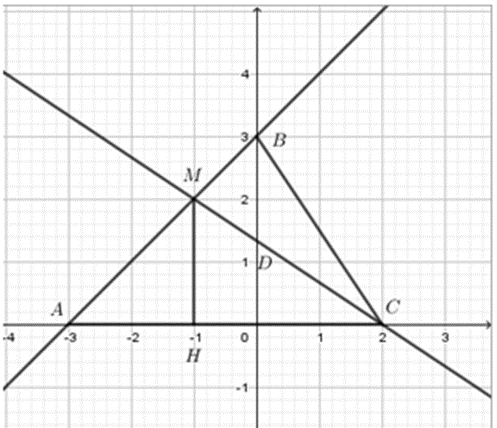
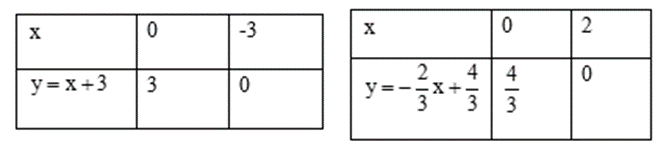
Xét phương trình hoành độ giao điểm:
$x + 3 = - \dfrac{2}{3}x + \dfrac{4}{3} \Leftrightarrow 3x + 9 = - 2x + 4 \Leftrightarrow 5x = - 5 \Leftrightarrow x = - 1 \Rightarrow y = 2$
Do đó giao điểm của $2$ đường thẳng đã cho là $M\left( { - 1;2} \right)$
$\begin{array}{l}d \cap Ox = A( - 3;0) \Rightarrow OA = 3\\d' \cap Ox = C(2;0) \Rightarrow OC = 2\\d \cap Oy = B(0;3) \Rightarrow OB = 3\\d' \cap Oy = D\left( {0;\dfrac{4}{3}} \right)\\ \Rightarrow AC = OA + OC = 3 + 2 = 5\\{S_{\Delta ABC}} = \dfrac{1}{2}AC.OB = \dfrac{1}{2}.5.3 = \dfrac{{15}}{2}(dvdt)\end{array}$
Gọi $H$ là hình chiếu của $M$ trên $Ox$
$\begin{array}{l} \Rightarrow MH = |{y_M}| = 2\\{S_{\Delta AMC}} = \dfrac{1}{2}MH.AC = \dfrac{1}{2}.2.5 = 5(dvdt)\\{S_{\Delta BMC}} = {S_{\Delta ABC}} - {S_{\Delta AMC}} = \dfrac{{15}}{2} - 5 = \dfrac{5}{2}(dvdt)\end{array}$
Hướng dẫn giải:
- Lập bảng giá trị để xác định 2 điểm thuộc đường thẳng.
- Xác định giao điểm 2 đường thẳng đã cho
- Tính độ dài các đoạn thẳng cần thiết
- Dựng đường cao của tam giác được tạo thành
- Tính diện tích các tam giác phụ được tạo thành
- Tính diện tích tam giác theo yêu cầu đề bài.
