Bốn điểm \(A,B\),\(C,D\) trong không khí tạo thành hình chữ nhật \(ABCD\) cạnh \(AD = 3cm\), \(AB = 4cm\). Các điện tích \({q_1},{q_2},{q_3}\) đặt lần lượt tại \(A,B,C\). Biết \({q_2} =  - 12,{5.10^{ - 8}}C\) và cường độ điện trường tại \(D\) bằng \(0.\) Tính \({q_1},{q_3}\).

Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} \) và \(\overrightarrow {{E_3}} \) lần lượt là cường độ điện trường do \({q_1},{q_2},{q_3}\) gây ra tại \(D\).

Điều kiện để cường độ điện trường tổng hợp tại \(D\) bằng \(0\) là: \(\overrightarrow {{E_1}}  + \overrightarrow {{E_2}}  + \overrightarrow {{E_3}}  = \overrightarrow 0 \)

Do \({q_2} < 0\) nên \(\overrightarrow {{E_2}} \) hướng về \(B\)  như hình.

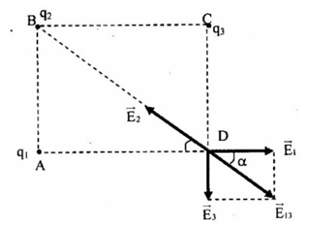
Muốn cường độ điện trường tổng hợp tại \(D\) bằng \(0\) thì \(\overrightarrow {{E_{13}}} \) phải cùng phương ngược chiều và có độ lớn bằng \({E_2}\).

Do đó, \(\overrightarrow {{E_1}} ,\overrightarrow {{E_3}} \) và \(\overrightarrow {{E_{1,3}}} \) có phương chiều như hình vẽ trên.

 Từ hình vẽ, ta có: 

Với \(\left\{ \begin{array}{l}\cos \alpha  = \dfrac{{AD}}{{\sqrt {A{D^2} + A{B^2}} }} = \dfrac{3}{5}\\\sin \alpha  = \dfrac{{AB}}{{\sqrt {A{D^2} + A{B^2}} }} = \dfrac{4}{5}\end{array} \right.\)

Lại có, \({E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{A{D^2}}} = {9.10^9}\dfrac{{12,{{5.10}^{ - 8}}}}{{0,{{05}^2}}} = 450000V/m = {45.10^4}V/m\)

Thay vào (1), ta được: \(\left\{ \begin{array}{l}{E_1} = {45.10^4}.\dfrac{3}{5} = {27.10^4}V/m\\{E_3} = {45.10^4}.\dfrac{4}{5} = {36.10^4}V/m\end{array} \right.\)

Lại có: \(\left\{ \begin{array}{l}{E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{D^2}}} \Rightarrow \left| {{q_1}} \right| = 2,{7.10^{ - 8}}C\\{E_3} = k\dfrac{{\left| {{q_3}} \right|}}{{C{D^2}}} \Rightarrow \left| {{q_3}} \right| = 6,{4.10^{ - 8}}C\end{array} \right.\)

Từ hình, thấy các véc-tơ \(\overrightarrow {{E_1}} ,\overrightarrow {{E_3}} \) hướng ra xa các điện tích nên \({q_1}\) và \({q_3}\) là các điện tích dương, do đó ta suy ra: \(\left\{ \begin{array}{l}{q_1} = 2,{7.10^{ - 8}}C\\{q_2} = 6,{4.10^{ - 8}}C\end{array} \right.\)