I. Kiến thức cần nhớ

II. Dạng toán: Tính giá trị các phép trừ có nhớ trong phạm vi 20 bằng cách đếm bớt
Ví dụ 1:
a) Tính 11 – 5.
b) Tính 16 – 8.
Giải:
a) Đếm bớt 5 bắt đầu từ 11 :
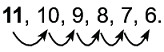
Vậy: 11 – 5 = 6.
b) Đếm bớt 8 bắt đầu từ 16:
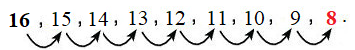
Vậy: 16 – 8 = 8.
Ví dụ 2: Số?
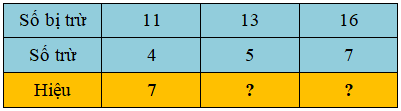
Phương pháp giải:
Áp dụng công thức: Số bị trừ – Số trừ = Hiệu.
Giải:
Ta có: 13 – 5 = 8
16 – 7 = 9
Vậy ta có bảng kết quả như sau:
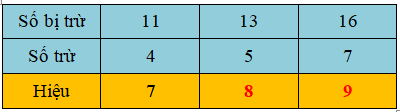
Ví dụ 3: Nối phép tính ở cột bên trái với kết quả ở cột bên phải.
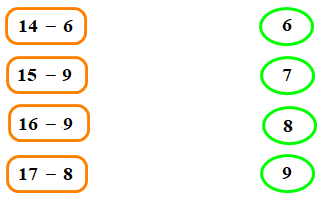
Giải:
Ta có:
14 – 6 = 8 15 – 9 = 6
16 – 9 = 7 17 – 8 = 9
Vậy ta ghép nối phép tính với kết quả tương ứng như sau:
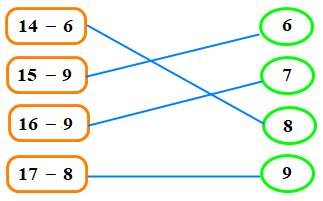
III. Dạng toán: Tính giá trị biểu thức
Biểu thức chỉ có phép cộng và phép trừ thì thực hiện các phép tính lần lượt từ trái sang phải.
Ví dụ 1: Tính: 13 – 9 + 4.
Giải:
13 – 9 + 4 = 4 + 4 = 8.
Ví dụ 2: Tính: 15 – 7 – 6.
Giải:
15 – 7 – 6 = 8 – 6 = 2.
IV. Dạng toán: So sánh
- Tính giá trị hai vế (nếu cần) rồi so sánh kết quả với nhau.
- Cách so sánh các số có hai chữ số:
• Số nào có chữ số hàng chục lớn hơn thì lớn hơn.
• Nếu hai số có chữ số hàng chục bằng nhau thì so sánh chữ số hàng đơn vị, số nào có chữ số hàng đơn vị lớn hơn thì lớn hơn.
Ví dụ: Điền dấu (>, <. =) thích hợp vào chỗ chấm
16 – 9 ... 7 18 – 9 ... 15 – 6
14 – 5 ... 8 13 – 5 ... 17 – 8
Giải:
\(\underbrace {16 - 9}_7\;\;\,\, = \,\,\,\,7\;\) \(\underbrace {18 - 9}_9\;\;\;\, = \;\;\;\underbrace {15 - 6}_9\)
\(\underbrace {14 - 5}_9\;\;\; > \;\;\,\,8\) \(\underbrace {13 - 5}_8\;\;\; < \,\,\,\;\underbrace {17 - 8}_9\)
V. Dạng toán: Toán có lời văn
- Đọc và phân tích đề bài.
- Tìm cách giải cho bài toán.
- Trình bày lời giải.
- Kiểm tra lại cách giải và kết quả của bài toán.
Ví dụ: Lan hái được 12 bông hoa, Mi hái được 8 bông hoa. Hỏi Lan hái được nhiều hơn Mi bao nhiêu bông hoa?
Giải:
Lan hái được nhiều hơn Mi số bông hoa là:
12 – 8 = 4 (bông hoa)
Đáp số: 4 bông hoa.

