Câu hỏi:
2 năm trước
Vật sáng AB đặt song song với một màn M, cách màn một đoạn L = 45 cm. Giữa vật và màn có một thấu kính hội tụ song song với vật và màn, trục chính của thấu kính đi qua A. Giữ cố định vật và màn, di chuyển thấu kính giữa vật và màn thì thấy có hai vị trí thấu kính cho hai ảnh trên màn, ảnh này gấp k = 4 lần ảnh kia. Tiêu cự thấu kính là
Trả lời bởi giáo viên
Đáp án đúng: c
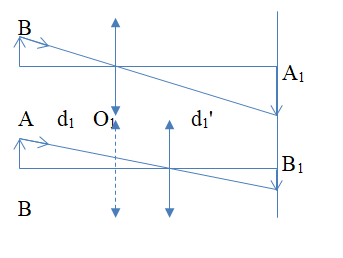
+ Khoảng cách vật và màn cố định, giữa vật và màn có hai vị trí thấu kính cho ảnh rõ nét trên màn thì theo nguyên lý về tính thuận nghịch của sự truyền ánh sáng, hai vị trí này phải có tính chất đối xứng, tức là:
\({d_1}' = {d_2}\)và \({d_2}' = {d_1}\) (1)
+ Theo giả thiết: \(k = \frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = 4\)
+ Lại có: \(k = \frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = \frac{{\overline {{A_1}{B_1}} }}{{\overline {{A_2}{B_2}} }} = \frac{{\overline {{A_1}{B_1}} }}{{\overline {AB} }}.\frac{{\overline {AB} }}{{\overline {{A_2}{B_2}} }} = \frac{{{k_1}}}{{{k_2}}}\) (2)
+ \({k_1} = - \frac{{{d_1}'}}{{{d_1}}};{k_2} = - \frac{{{d_2}'}}{{{d_2}}}\) (3)
Từ (1); (2) và (3) ta có: \(\sqrt k = \frac{{{d_1}'}}{{{d_1}}}\)
\( \to \frac{{\sqrt k }}{{{d_1}'}} = \frac{1}{{{d_1}}}\)
Theo tính chất phân thức:
\(\frac{{\sqrt k }}{{{d_1}'}} = \frac{1}{{{d_1}}} = \frac{{\sqrt k + 1}}{L}\) (*)
+ Theo công thức thấu kính:
\(f = \frac{{{d_1}{d_1}'}}{{{d_1} + {d_1}'}} = \frac{{{d_1}{d_1}'}}{L}\) (**)
Từ (*) và (**), ta được: \(f = \frac{{L\sqrt k }}{{{{\left( {\sqrt k + 1} \right)}^2}}}\)
Thay số, được: \(f = 10cm\)
Hướng dẫn giải:
+ Sử dụng biểu thức xác định hệ số phóng đại: \(k = - \frac{{d'}}{d} = \frac{{A'B'}}{{AB}}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính khoảng cách vật - ảnh: \(L = d + d'\)
