Trong thí nghiệm giao thoa sóng ở mặt nước với hai nguồn cùng pha đặt tại hai điểm A và B. Biết sóng truyền trên mặt nước với bước sóng là λ, độ dài đoạn thẳng AB là 5,8λ. Ở mặt nước, gọi (Δ) là đường trung trực của AB; M, N, P, Q là bốn điểm không thuộc (Δ) mà phần tử nước tại bốn điểm đó đều dao động với biên độ cực đại, cùng pha với nguồn và gần (Δ) nhất. Trong bốn điểm M, N, P, Q khoảng cách giữa hai điểm xa nhau nhất có giá trị là
Trả lời bởi giáo viên
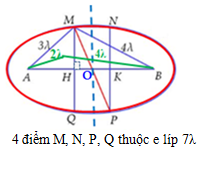
+ M, N, P, Q thuộc hình chữ nhật , khoảng cách gần nhất bằng độ dài đoạn MN. Ta chỉ xét điểm M.
+ M dao động với biên độ cực đại: {d_2} - {d_1} = k\lambda
+ M dao động cùng pha với nguồn: \left[ \begin{array}{l}\left\{ \begin{array}{l}{d_2} - {d_1} = {k_{le}}\lambda \\{d_2} + {d_1} = {n_{le}}\lambda > 5,8\lambda \end{array} \right.\\\left\{ \begin{array}{l}{d_2} - {d_1} = {k_{chan}}\lambda \\{d_2} + {d_1} = {n_{chan}}\lambda > 5,8\lambda \end{array} \right.\end{array} \right.
+ M gần Δ nhất thì \left[ \begin{array}{l}{d_2} - {d_1} = 1.\lambda ,{d_2} + {d_1} = 7\lambda \to \left\{ \begin{array}{l}{d_2} = 4\lambda \\{d_1} = 3\lambda \end{array} \right.\\{d_2} - {d_1} = 2.\lambda ,{d_2} + {d_1} = 6\lambda \to \left\{ \begin{array}{l}{d_2} = 4\lambda \\{d_1} = 2\lambda \end{array} \right.(loại)\end{array} \right.
+ Chọn \lambda = 1
=> \sqrt {{3^2} - {{(MH)}^2}} + \sqrt {{4^2} - {{(MH)}^2}} = 5,8 \\\to MH \approx 1,93 \\\to MQ \approx 3,86;MN \approx 1,21\\ \to MP \approx 4,05
Hướng dẫn giải:
+4 điểm không thuộc đường trung trựcΔ của đoạn thẳng nối hai nguồn dao động với biên độ cực đại, cùng pha với nguồn và gần Δ nhất tạo với nhau một hình chữ nhật
+ Xét điểm M dao động với biên độ cực đại: {d_2} - {d_1} = k\lambda
+ M dao động cùng pha với nguồn: \left[ \begin{array}{l}\left\{ \begin{array}{l}{d_2} - {d_1} = {k_{le}}\lambda \\{d_2} + {d_1} = {n_{le}}\lambda \end{array} \right.\\\left\{ \begin{array}{l}{d_2} - {d_1} = {k_{chan}}\lambda \\{d_2} + {d_1} = {n_{chan}}\lambda \end{array} \right.\end{array} \right.

