Câu hỏi:
2 năm trước
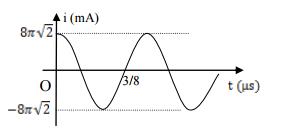
Trong một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Biên độ của cường độ dòng điện trong mạch là \({I_0} = 0,5\pi \sqrt 2 \) (A). Biết thời gian để cường độ dòng điện trong mạch giảm từ giá trị lớn nhất xuống đến một nửa giá trị lớn nhất là \(\dfrac{8}{3}\left( {\mu s} \right)\). Ở những thời điểm cường độ dòng điện trong mạch \(i{\rm{ }} = {\rm{ }}0\) thì điện tích trên tụ là
Trả lời bởi giáo viên
Đáp án đúng: a
+ Thời gian để cường độ dòng điện trong mạch giảm từ giá trị lớn nhất xuông đến 1 nửa giá trị lớn nhất là:
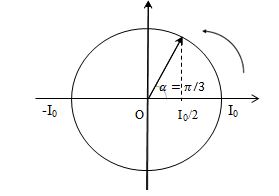
\(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{\pi }{3}.\dfrac{T}{{2\pi }} = \dfrac{T}{6} = \dfrac{8}{3}\mu s \Rightarrow T = 16\mu s\)
Ta có: \(\dfrac{{{i^2}}}{{I_0^2}} + \dfrac{{{q^2}}}{{Q_0^2}} = 1 \Rightarrow q = {Q_0}.\sqrt {1 - \dfrac{{{i^2}}}{{I_0^2}}} = \dfrac{{{I_0}}}{\omega }.\sqrt {1 - \dfrac{{{i^2}}}{{I_0^2}}} = \dfrac{{{I_0}.T}}{{2\pi }}.\sqrt {1 - \dfrac{{{i^2}}}{{I_0^2}}} \)
\(i = 0 \Rightarrow q = \dfrac{{{I_0}T}}{{2\pi }} = 4\sqrt 2 \mu C\)
Hướng dẫn giải:
Sử dụng vòng tròn lượng giác và công thức vuông pha giữa điện tích và cường độ dòng điện \(\dfrac{{{i^2}}}{{I_0^2}} + \dfrac{{{q^2}}}{{Q_0^2}} = 1\)
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
