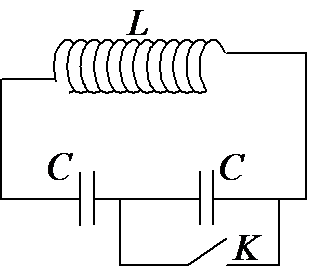
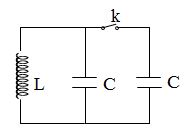
Trong mạch dao động LC có điện trở thuần không đáng kể, chu kỳ dao động của mạch là \(T{\rm{ }} = {\rm{ }}{10^{ - 6}}s\), khoảng thời gian ngắn nhất để năng lượng điện trường lại bằng năng lượng từ trường :
Trả lời bởi giáo viên
Đề cho: \({W_C} = {W_L}\)
W = WC + WL = \(\dfrac{{{q^2}}}{{2C}}\) + \(\dfrac{{L{i^2}}}{2}\)
<=>\(\dfrac{{{q_0}^2}}{{2C}}\) =\(\dfrac{{{q^2}}}{{2C}}\) +\(\dfrac{{{q^2}}}{{2C}}\)
<=> \(q = \dfrac{{\sqrt 2 }}{2}{q_0}\)
Hình vẽ vòng lượng gíác cho ta góc quét từ lúc năng lượng điện trường cực đại đến năng lượng điện trường bàng năng lượng từ rường là: \(\Delta \varphi = \dfrac{\pi }{4}\)
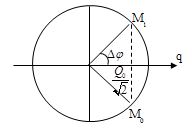
Vậy từ lúc năng lượng điện trường bằng năng lượng từ trường đến lúc năng lượng điện trường bàng năng lượng từ trường lần kế tiếp là:
\(\Delta \varphi ' = \dfrac{\pi }{2}\) ( xem hình vẽ từ M0 đến M1)
Ứng với thời gian \(t = \dfrac{T}{4} = \dfrac{{{{10}^{ - 6}}}}{4} = {2,5.10^{ - 7}}s\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \dfrac{1}{2}C{U_0}^2 = \dfrac{{{Q_0}^2}}{{2C}} = \dfrac{{LI{{_0^{}}^2}}}{2}\)
+ Vận dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)