Câu hỏi:
2 năm trước
Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;3; - 3} \right),B\left( {3;0;3} \right)\). Biết mặt phẳng (P) đi qua điểm A và cách B một khoảng lớn nhất. Tính khoảng cách đó.
Chỉ được điền các số nguyên và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
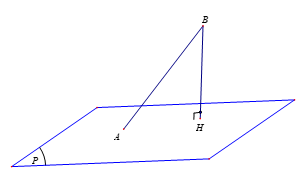
Gọi H là hình chiếu của B trên mặt phẳng (P) khi đó ta có BH là khoảng cách từ điểm B đến mặt phẳng (P). Ta luôn có BH\( \le \)AB do đó khoảng cách từ B đến mặt phẳng (P) lớn nhất khi H ≡ A, hay \(d\left( {B;\left( P \right)} \right) = BA = \sqrt {{2^2} + {{\left( { - 3} \right)}^2} + {6^2}} = 7\)
Hướng dẫn giải:
- Gọi H là hình chiếu của B trên mặt phẳng (P)
- Tính khoảng cách lớn nhất từ B đến (P)


