Điền số nguyên hoặc phân số dạng a/b vào chỗ trống
Cho tứ diện $A B C D$. Các điểm $P, Q$ lần lượt là trung điểm của $A B$ và $C D$; điểm \(R\) nằm trên cạnh $B C$ sao cho \(BR = 2RC\). Gọi \(S\) là giao điểm của mặt phẳng \((PQR)\) và cạnh $A D$. Tỉ số \(\dfrac{{SA}}{{SD}}\) bằng:
Trả lời bởi giáo viên
Cho tứ diện $A B C D$. Các điểm $P, Q$ lần lượt là trung điểm của $A B$ và $C D$; điểm \(R\) nằm trên cạnh $B C$ sao cho \(BR = 2RC\). Gọi \(S\) là giao điểm của mặt phẳng \((PQR)\) và cạnh $A D$. Tỉ số \(\dfrac{{SA}}{{SD}}\) bằng:
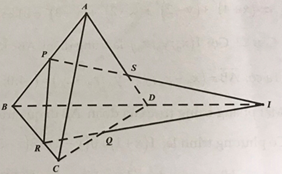
Gọi I là giao điểm của \({\rm{BD}}\) và \(R{\rm{Q}}\). Nối \(P\) với \({\rm{I}}\), cắt \({\rm{AD}}\) tại \({\rm{S}}\). Xét tam giác \({\rm{BCD}}\) bị cắt bởi \({\rm{IR}}\), ta có
\(\dfrac{{{\rm{DI}}}}{{{\rm{IB}}}} \cdot \dfrac{{{\rm{BR}}}}{{{\rm{RC}}}} \cdot \dfrac{{{\rm{CQ}}}}{{{\rm{QD}}}} = 1 \Leftrightarrow \dfrac{{{\rm{DI}}}}{{{\rm{IB}}}} \cdot 2 \cdot 1 = 1 \Leftrightarrow \dfrac{{{\rm{DI}}}}{{{\rm{IB}}}} = \dfrac{1}{2}\)
Xét tam giác \({\rm{ABD}}\) bị cắt bởi \({\rm{PI}}\), ta có
\(\dfrac{{{\rm{AS}}}}{{{\rm{SD}}}} \cdot \dfrac{{{\rm{DI}}}}{{{\rm{IB}}}} \cdot \dfrac{{{\rm{BP}}}}{{{\rm{PA}}}} = 1 \Leftrightarrow \dfrac{{{\rm{SA}}}}{{{\rm{SD}}}} \cdot \dfrac{1}{2} \cdot 1 = 1 \Leftrightarrow \dfrac{{{\rm{SA}}}}{{{\rm{SD}}}} = 2\)
Hướng dẫn giải:
Dựa vào \(\dfrac{{{\rm{DI}}}}{{{\rm{IB}}}} \cdot \dfrac{{{\rm{BR}}}}{{{\rm{RC}}}} \cdot \dfrac{{{\rm{CQ}}}}{{{\rm{QD}}}} = 1\) và \(\dfrac{{{\rm{AS}}}}{{{\rm{SD}}}} \cdot \dfrac{{{\rm{DI}}}}{{{\rm{IB}}}} \cdot \dfrac{{{\rm{BP}}}}{{{\rm{PA}}}} = 1\) để tính tỉ số \(\dfrac{{SA}}{{SD}}\).
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 3 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
