Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(M\) thuộc mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 9\) và ba điểm \(A\left( {1;0;0} \right)\), \(B\left( {2;1;3} \right)\), \(C\left( {0;2; - 3} \right)\). Biết rằng quỹ tích điểm \(M\) thỏa mãn \(M{A^2} + 2\overrightarrow {MB} .\overrightarrow {MC}  = 8\) là một đường tròn cố định, tính bán kính \(r\) của đường tròn này.

Gọi \(M\left( {x;y;z} \right)\). Ta có \(\left\{ \begin{array}{l}\overrightarrow {MA}  = \left( {1 - x; - y; - z} \right)\\\overrightarrow {MB}  = \left( {2 - x;1 - y;3 - z} \right)\\\overrightarrow {MC}  = \left( { - x;2 - y; - 3 - z} \right)\end{array} \right.\).

\(\begin{array}{l} \Rightarrow M{A^2} + 2\overrightarrow {MB} .\overrightarrow {MC}  = 8\\ \Leftrightarrow {\left( {1 - x} \right)^2} + {y^2} + {z^2} - 2x\left( {2 - x} \right) + 2\left( {1 - y} \right)\left( {2 - y} \right) + 2\left( {3 - z} \right)\left( { - 3 - z} \right) = 8\\ \Leftrightarrow {x^2} + {y^2} + {z^2} - 2x + 1 - 4x + 2{x^2} + 2\left( {2 - 3y + {y^2}} \right) - 2\left( {9 - {z^2}} \right) = 8\\ \Leftrightarrow {x^2} + {y^2} + {z^2} - 2x + 1 - 4x + 2{x^2} + 4 - 6y + 2{y^2} - 18 + 2{z^2} = 8\\ \Leftrightarrow 3{x^2} + 3{y^2} + 3{z^2} - 6x - 6y - 21 = 0\\ \Leftrightarrow {x^2} + {y^2} + {z^2} - 2x - 2y - 7 = 0\,\,\left( {S'} \right)\end{array}\)

\( \Rightarrow M \in \left( {S'} \right)\) là mặt cầu tâm \(I'\left( {1;1;0} \right)\), bán kính \(R' = \sqrt {1 + 1 + 7}  = 3\).

Hơn nữa, \(M \in \left( S \right)\) có tâm \(I\left( {3;3;2} \right)\), bán kính \(R = 3\).

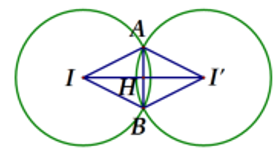
Ta có: \(II' = \sqrt {{2^2} + {2^2} + {2^2}}  = 2\sqrt 3  < R + R'\).

\( \Rightarrow M = \left( S \right) \cap \left( {S'} \right)\) là một đường tròn có bán kính \(r = AH\).

Dễ thấy \(\Delta AII'\) cân tại \(A\) nên \(H\) là trung điểm của \(II'\) \( \Rightarrow IH = \dfrac{1}{2}II' = \sqrt 3 \).

Vậy \(r = AH = \sqrt {A{I^2} - I{H^2}}  = \sqrt {{3^2} - {{\left( {\sqrt 3 } \right)}^2}}  = \sqrt 6 \).