Điền số nguyên hoặc phân số dạng a/b vào chỗ trống
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi $M, N$ lần lượt là trung điểm của $A B, A D$ và \(G\) là trọng tâm tam giác $S B D$. Mặt phẳng \(({\rm{MNG}})\) cắt $S C$ tại điểm \(H\). Tỉ số \(\dfrac{{SH}}{{SC}}\) bằng:
Trả lời bởi giáo viên
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi $M, N$ lần lượt là trung điểm của $A B, A D$ và \(G\) là trọng tâm tam giác $S B D$. Mặt phẳng \(({\rm{MNG}})\) cắt $S C$ tại điểm \(H\). Tỉ số \(\dfrac{{SH}}{{SC}}\) bằng:
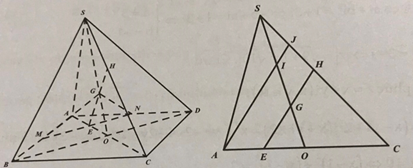
Trong mặt phẳng \((ABCD)\), gọi \(E = MN \cap AC\). Trong mặt phẳng \((SAC)\), gọi \(H = EG \cap SC\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{H \in EG;EG \subset (MNG)}\\{H \in SC}\end{array} \Rightarrow H = SC \cap (MNG)} \right.\).
Gọi \(I,J\) lần lượt là trung điểm của $SG$ và $SH$.
Ta có \(\left\{ {\begin{array}{*{20}{l}}{{\rm{IJ}}//{\rm{HG}}}\\{{\rm{IA}}//{\rm{GE}}}\end{array} \Rightarrow {\rm{A}},{\rm{I}},{\rm{J}}} \right.\) thẳng hàng.
Xét \(\Delta {\rm{ACJ}}\) có \({\rm{EH}}//{\rm{AJ}} \Rightarrow \dfrac{{{\rm{CH}}}}{{{\rm{HJ}}}} = \dfrac{{{\rm{CE}}}}{{{\rm{EA}}}} = 3 \Rightarrow {\rm{CH}} = 3{\rm{HJ}}\).
Lại có \(SH = 2HJ\) nên \(SC = 5HJ\). Vậy \(\dfrac{{SH}}{{SC}} = \dfrac{2}{5}\).
Hướng dẫn giải:
Gọi \(I,J\) lần lượt là trung điểm của $SG$ và $SH$.
Từ đó cm A,I,J thẳng hàng
Áp dụng định lí Ta-lét để tính tỉ lệ \(\dfrac{{{\rm{CH}}}}{{{\rm{HJ}}}}\)từ đó suy ra tỉ lệ \(\dfrac{{SH}}{{SC}}\)

 (Nguồn: ourwordindata.org)
(Nguồn: ourwordindata.org)