Câu hỏi:
3 năm trước
Trong không gian \(Oxyz\) với hệ tọa độ , cho hai điểm \(I\left( { - 1;1;1} \right)\) và \(A\left( {1;3;2} \right)\) và Gọi là hình chiếu vuông góc của A trên mặt phẳng \(\left( P \right):x + 2y - 2z + 1 = 0\). Tính diện tích S tam giác IHA. (Làm tròn đến hàng đơn vị)
Chỉ điền số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
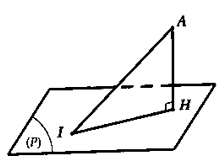
Ta có: \(IA = 3,AH = d\left( {A;\left( P \right)} \right) = \)\(\dfrac{{\left| {1 + 2.3 - 2.2 + 1} \right|}}{3} = \dfrac{4}{3}\) và \(I \in \left( P \right)\)
Tam giác IHA vuông tại H suy ra:
\(IH = \sqrt {I{A^2} - A{H^2}} = \dfrac{{\sqrt {65} }}{3}\)
Vậy \(S = \dfrac{1}{2}.AH.IH = \dfrac{{2\sqrt {65} }}{9} \approx 2\)
Hướng dẫn giải:
- Tính IA, AH
- Tính IH và diện tích S.


