Cho hình chóp $S . A B C D$ có đáy là hình vuông cạnh \(a\sqrt 2 ,SA\) vuông góc với mặt phẳng đáy, \(SA = a\sqrt 3 \). Góc giữa hai mặt phẳng \((SBD)\) và \((ABCD)\) bằng:
Trả lời bởi giáo viên
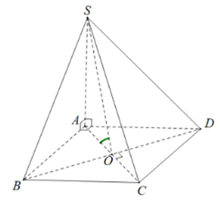
Gọi \(O = AC \cap BD\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BD \bot SA}\\{BD \bot AC}\end{array} \Rightarrow BD \bot (SAC)} \right.\).
Do đó:
\(\left\{ {\begin{array}{*{20}{l}}{BD \bot (SAC)}\\{(SBD) \cap (ABCD) = BD}\\{(SAC) \cap (SBD) = SO}\\{(SAC) \cap (ABCD) = AC}\end{array} \Rightarrow \widehat {((SBD),(ABCD)}) = \widehat {(SO,AC)} = \widehat {SOA}.} \right.\)
Xét hình vuông $A B C D$ ta có: \(OA = \dfrac{{AC}}{2} = \dfrac{{AB\sqrt 2 }}{2} = \dfrac{{a\sqrt 2 \sqrt 2 }}{2} = a\).
Xét vuông tại \(A\), ta có: \(\tan \widehat {SOA} = \dfrac{{SA}}{{OA}} = \dfrac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SOA} = {60^\circ }\).
Hướng dẫn giải:
$\widehat {((SBD),(ABCD)}) = \widehat {(SO,AC)}$


