Cho hình chóp S.ABCD có đáy ${\rm{ABCD}}$ là hình vuông cạnh ${\rm{a}},{\rm{SA}}$ vuông góc với mặt phẳng $({\rm{ABCD}})$ và ${\rm{SA}} = {\rm{a}}$. Gọi ${\rm{E}}$ là trung điểm của cạnh ${\rm{CD}}$. Tính theo a khoảng cách từ điểm $S$ đến đường thẳng ${\rm{BE}}$

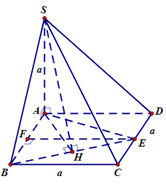
Vì ${\rm{SA}} \bot ({\rm{ABCD}})$, trong mặt phẳng $({\rm{ABCD}})$ nếu dựng ${\rm{AH}} \bot {\rm{BE}}$ tại ${\rm{H}}$ thì ${\rm{SH}} \bot {\rm{BE}}$ (định lí 3 đường vuông góc).

Tức là khoảng cách từ điểm $S$ đến đường thẳng $BE$ bằng đoạn ${\rm{SH}}$. Ta có:

Mà $BE = \sqrt {B{C^2} + C{E^2}} = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}$

Nên ${\rm{AH}} = \dfrac{{{{\rm{a}}^2}}}{{{\rm{BE}}}} = \dfrac{{2{\rm{a}}}}{{\sqrt 5 }}$, mà $\Delta {\rm{SAH}}$ vuông tại ${\rm{A}}$, nên:

${\rm{SH}} = \sqrt {{\rm{S}}{{\rm{A}}^2} + {\rm{A}}{{\rm{H}}^2}} = \sqrt {{{\rm{a}}^2} + \dfrac{{4{{\rm{a}}^2}}}{5}} = \dfrac{{3{\rm{a}}}}{{\sqrt 5 }} = \dfrac{{3{\rm{a}}\sqrt 5 }}{5}$

Vậy $d(S,BE) = \dfrac{{3a\sqrt 5 }}{5}.$