Câu hỏi:
2 năm trước
Điền số nguyên hoặc phân số dạng a/b vào chỗ trống
Cho hình chóp SABCD có đáy C′ là điểm trên cạnh SC sao cho SC′=23SC. Thiết diện của hình chóp với mặt phẳng (ABC′) là một đa giác m cạnh. Giá trị của m bằng:
Trả lời bởi giáo viên
Đáp án:
Cho hình chóp SABCD có đáy C′ là điểm trên cạnh SC sao cho SC′=23SC. Thiết diện của hình chóp với mặt phẳng (ABC′) là một đa giác m cạnh. Giá trị của m bằng:
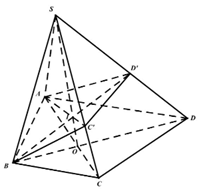
Gọi O=AC∩BD và I=ACC′∩SO; Kéo dài BI cắt SD tại D′.
Khi đó (ABC′)∩(ABCD)=AB;(ABC′)∩(SAB)=AB;
(ABC′)∩(SBC)=BC′
và (ABC′)∩(SAD)=AD′;(ABC′)∩(SBD)=C′D′
Suy ra thiết diện là tứ giác ABC′D′ nên m=4.
Hướng dẫn giải:
Gọi O=AC∩BD và I=ACC′∩SO; Kéo dài BI cắt SD tại D′.


