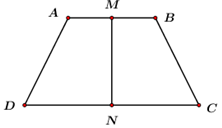
Trong không gian, cho hình thang cân \(ABCD,\,\,AB//CD,\) \(AB = 3a,\,\,CD = 6a,\) đường cao \(MN = 2a,\) với \(M,\,\,N\) lần lượt là trung điểm cảu \(AB\) và \(CD.\) Khi quay hình thang cân quang trục đối xứng \(MN\) thì được một hình nón cụt có diện tích xung quanh là:

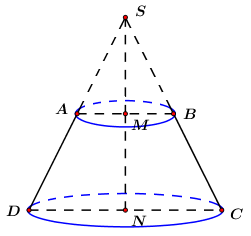
Kéo dài AD và BC cắt nhau tại S.

Quay tam giác SCD quanh trục SN được hình nón (N) đỉnh S, đáy là đường tròn đường kính CD.

Gọi hình nón đỉnh S, đáy là đường tròn đường kính AB là (M).

Theo định lý Talet ta có: \(\dfrac{{SA}}{{SD}} = \dfrac{{SM}}{{SN}} = \dfrac{{AB}}{{AD}} = \dfrac{{3a}}{{6a}} = \dfrac{1}{2}\)

\( \Rightarrow \dfrac{{SM}}{{SN}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{SM}}{{SM + 2a}} = \dfrac{1}{2}\) \( \Leftrightarrow 2SM = SM + 2a\)\( \Leftrightarrow SM = 2a\)

\( \Rightarrow SN = SM + MN = 4a.\)

Áp dụng định lý Pitago cho các tam giác \(SAM,\,\,SDN\) vuông tại \(M,\,\,N\) ta có:

\(\left\{ \begin{array}{l}S{A^2} = S{M^2} + A{M^2}\\S{D^2} = S{N^2} + D{N^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}S{A^2} = 4{a^2} + {\left( {\dfrac{{3a}}{2}} \right)^2} = \dfrac{{25{a^2}}}{4}\\S{D^2} = {\left( {4a} \right)^2} + {\left( {\dfrac{{6a}}{2}} \right)^2} = 25{a^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}SA = \dfrac{{5a}}{2}\\SD = 5a\end{array} \right..\)

\( \Rightarrow \) Diện tích xung quanh hình chóp cụt cần tính là:

\(\begin{array}{l}{S_{xq\,\,\left( N \right)}} - {S_{xq\,\,\left( M \right)}} = \pi .DN.SD - \pi .SA.AM\\ = \pi .5a.3a - \pi .\dfrac{{5a}}{2}.\dfrac{{3a}}{2} = \dfrac{{45\pi {a^2}}}{4} = 11,25\pi {a^2}.\end{array}\)