Câu hỏi:
2 năm trước
Trên tia đối của tia \(DE\) lấy điểm \(M\) sao cho \(DM = DC\). Nối \(AE,\) so sánh số đo \(\widehat {AEC};\widehat {EAM}\).
Trả lời bởi giáo viên
Đáp án đúng: c
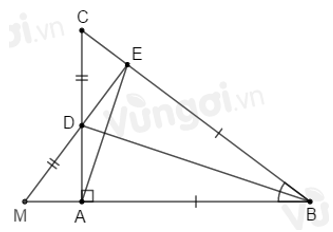
Sử dụng kết quả câu trước \(\Delta ADM = \Delta EDC\) suy ra \(AD = ED;\,AM = EC\) (các cạnh tương ứng).
Ta có: \(AD = ED\,\,\,\,(1)\)
\(DC = DM\,\,\,(2)\)
Cộng (1) và (2) theo vế với vế ta được: \(AD + DC = ED + DM\) hay \(AC = EM\).
Xét \(\Delta AEC\) và \(\Delta EAM\) có:
\(AE\) cạnh chung
\(EC = AM\,(cmt)\)
\(AC = EM\,(cmt)\)
\( \Rightarrow \Delta AEC = \Delta EAM\,(c.c.c)\)
\( \Rightarrow \widehat {AEC} = \widehat {EAM}\) (hai góc tương ứng).
Hướng dẫn giải:
- Sử dụng kết quả câu trước \(\Delta ADM = \Delta EDC\) suy ra \(AD = ED;\,AM = EC\) (các cạnh tương ứng).
- Sử dụng trường hợp bằng nhau thứ nhất của tam giác để chứng minh \(\Delta AEC = \Delta EAM\), từ đó suy ra điều phải chứng minh.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
