Câu hỏi:
1 năm trước
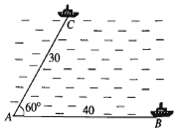
Trên biển, tàu B ở vị trí cách tàu A 53km về hướng \( N{34^o}E\). Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50 km/h để đuổi kịp tàu B.
Với hướng chuyển động đó thì sau bao lâu tàu A đuổi kịp tàu B?
Trả lời bởi giáo viên
Đáp án đúng: d
Xét tam giác ABC, ta có:
\( \begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\( \dfrac{a}{{\sin A}} = \dfrac{c}{{\sin C}} \Rightarrow a = \dfrac{{c.\sin A}}{{\sin C}}\)
Mà \( \left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \dfrac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\( \begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.
Hướng dẫn giải:
Bước 1: Tính góc C
Bước 2: Áp dụng định lí sin \( \dfrac{a}{{\sin \alpha }} = \dfrac{c}{{\sin C}}\) để suy ra t (thời gian đi cho đến khi gặp nhau)
Câu hỏi khác
- Bài tập trắc nghiệm Giá trị lượng giác của một góc từ 0 đến 180. Định lí côsin và định lí sin trong tam giác môn Toán lớp 10 CD có lời giải
- Bài tập trắc nghiệm Tổng và hiệu của hai vectơ môn Toán lớp 10 CD có lời giải
- Bài tập trắc nghiệm Tích của một số với một vectơ môn Toán lớp 10 CD có lời giải
- Bài tập trắc nghiệm Khái niệm vectơ môn Toán lớp 10 CD có lời giải
- Bài tập trắc nghiệm Giải tam giác môn Toán lớp 10 CD có lời giải
