Câu hỏi:
1 năm trước
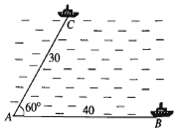
Trên biển, tàu B ở vị trí cách tàu A 53km về hướng \( N{34^o}E\). Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50 km/h để đuổi kịp tàu B.
Hỏi tàu A cần phải chuyển động theo hướng nào?
Trả lời bởi giáo viên
Đáp án đúng: a
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \( \dfrac{a}{{\sin \alpha }} = \dfrac{b}{{\sin B}}\)
Trong đó: \( \left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\( \begin{array}{l} \Rightarrow \dfrac{{30t}}{{\sin \alpha }} = \dfrac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \dfrac{{30t.\sin {{124}^o}}}{{50t}} = \dfrac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \( \alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \( {30^o}\).
Hướng dẫn giải:
Tìm hướng chuyển động của A, tức là đi tính góc \( \alpha + {34^o}\)
Bước 1: Tính quãng đường BC, AC theo ẩn t (thời gian chạy cho đến khi gặp nhau)
Bước 2: Vận dụng định lí sin
\( \dfrac{a}{{\sin \alpha }} = \dfrac{b}{{\sin B}}\)
Để suy ra \( \sin \alpha \), từ đó suy ra hướng của tàu A.
Câu hỏi khác
- Bài tập trắc nghiệm Giá trị lượng giác của một góc từ 0 đến 180. Định lí côsin và định lí sin trong tam giác môn Toán lớp 10 CD có lời giải
- Bài tập trắc nghiệm Tổng và hiệu của hai vectơ môn Toán lớp 10 CD có lời giải
- Bài tập trắc nghiệm Tích của một số với một vectơ môn Toán lớp 10 CD có lời giải
- Bài tập trắc nghiệm Khái niệm vectơ môn Toán lớp 10 CD có lời giải
- Bài tập trắc nghiệm Giải tam giác môn Toán lớp 10 CD có lời giải
