Trả lời bởi giáo viên
Đáp án đúng: d
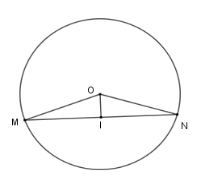
Xét $\left( O \right)$ có $OI \bot MN$ tại $I$ nên $I$ là trung điểm của dây $MN$ (đường kính vuông góc với dây thì đi qua trung điểm của dây đó) $ \Rightarrow MI = IN=\dfrac{MN}2 = \dfrac{{\sqrt 3 R}}{2}$
Xét tam giác $OIM$ vuông tại $I$, theo định lý Pytago ta có $O{I^2} = O{M^2} - M{I^2}$
$\Rightarrow OI = \sqrt {{R^2} - {{\left( {\dfrac{{\sqrt 3 R}}{2}} \right)}^2}} $$= \sqrt {{R^2} - \dfrac{{ 3 R^2}}{4}} =\sqrt { \dfrac{ R^2}{4}}= \dfrac{R}{2}$
Hướng dẫn giải:
Sử dụng liên hệ giữa đường kính và dây cung.
Sử dụng định lý Pytago.

