Câu hỏi:
2 năm trước
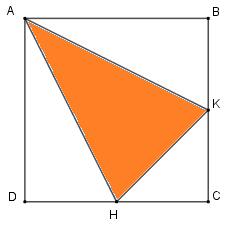
Tính diện tích hình tam giác \(AHK\). Biết hình vuông \(ABCD\) có cạnh \(16cm\) và \(BK = KC,\,\,DH = HC\).
Trả lời bởi giáo viên
Đáp án đúng:
C. \(96c{m^2}\)
Ta có \(ABCD\) là hình vuông cạnh \(16cm\) nên \(AB = BC = CD = AD = 16cm\).
Lại có theo đề bài \(BK = KC,\,\,DH = HC\) nên \(BK = KC = \,DH = HC = 16:2 = 8cm\).
Diện tích hình vuông \(ABCD\) là:
\(16 \times 16 = 256\;(c{m^2})\)
Diện tích hình tam giác \(ABK\) là:
\(16 \times 8:2 = 64\;(c{m^2})\)
Diện tích hình tam giác \(KCH\) là:
\(8 \times 8:2 = 32\;(c{m^2})\)
Diện tích hình tam giác \(ADH\) là:
\(16 \times 8:2 = 64\;(c{m^2})\)
Diện tích hình tam giác \(AHK\) là:
\(256 - (64 + 32 + 64) = 96\;(c{m^2})\)
Đáp số: \(96c{m^2}\).
Hướng dẫn giải:
Muốn tính diện tích hình tam giác \(AHK\) ta lấy diện tích hình vuông \(ABCD\) trừ đi tổng diện tích của ba hình tam giác vuông \(ABK,\,\,KCH\) và \(ADH\).
Trong một tam giác có:
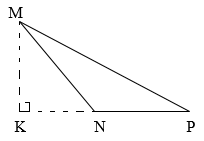
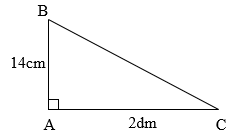
Độ dài cạnh đáy của hình tam giác có chiều cao \(24cm\) và diện tích là \(420c{m^2}\) là: 
Điền số thích hợp vào ô trống:
