Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y = - {x^3} + 2{x^2} - m$ cắt trục hoành tại đúng một điểm
Trả lời bởi giáo viên
Yêu cầu bài toán \( \Leftrightarrow \) phương trình $ - {x^3} + 2{x^2}-m\; = 0$ có đúng một nghiệm thực
\( \Leftrightarrow \) đường thẳng $y = m$ có đúng $1$ điểm chung với đồ thị hàm số: $y = f(x) = - {x^3} + 2{x^2}$
Lập bảng biến thiên của hàm số: $y = f(x) = - {x^3} + 2{x^2}$
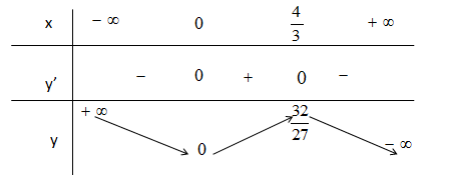
Dựa vào bảng biến thiên ta được kết quả: $m < 0$ hoặc $m > \dfrac{{32}}{{27}}$
Hướng dẫn giải:
Bước 1: Viết phương trình hoành độ giao điểm của đồ thị với trục hoành
Bước 2: Biện luận: Đồ thị cắt trục hoành tại đúng 1 điểm ó phương trình hoành độ giao điểm trên có đúng 1 nghiệm duy nhất.
Bước 3: Cô lập m sang 1 vế và ta xét bảng biến thiên cho hàm số bên vế kia
Bước 4: Dựa vào bảng biến thiên và kết luận