Câu hỏi:
2 năm trước
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có số nghiệm của phương trình đã cho là số giao điểm của đồ thị (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ và đường thẳng d: $y = - m$.
Xét hàm số (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ có: $y' = 5{x^4} + 3{x^2} + \dfrac{1}{{2\sqrt {1 - x} }} > 0\,\,\forall x \in \left( { - \infty ;1} \right)$$ \Rightarrow $ hàm số luôn đồng biến trên $\left( { - \infty ;1} \right]$.
Lại có $y\left( 1 \right) = 2$.
Ta có BBT:
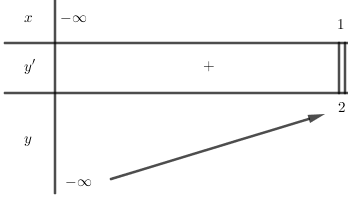
Theo BBT ta thấy pt có nghiệm $ \Leftrightarrow - m \leqslant 2 \Leftrightarrow m \geqslant - 2$.
Hướng dẫn giải:
- Nêu mối quan hệ giữa số nghiệm của phương trình và số giao điểm của $d$ và $\left( C \right)$.
- Khảo sát hàm số $y = {x^5} + {x^3} - \sqrt {1 - x} $ trên $\left( { - \infty ;1} \right]$ và từ đó suy ra điều kiện của $m$.
