Tam giác \(ABC\) vuông tại $A,{\rm{ }}AB = AC = 2$. Độ dài vectơ $4\overrightarrow {AB} - \overrightarrow {AC} $bằng:
Trả lời bởi giáo viên
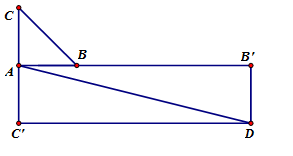
Vẽ $\overrightarrow {AB'} = 4\overrightarrow {AB} ;\,\,\,\,\,\,\overrightarrow {AC'} = - \overrightarrow {AC} $. Vẽ hình bình hành $AC'DB'$
Ta có: $\left| {4\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB'} + \overrightarrow {AC'} } \right| = \left| {\overrightarrow {AD} } \right| = AD$
Do đó $AD = \sqrt {A{{B'}^2} + A{{C'}^2}} = \sqrt {{8^2} + {2^2}} = 2\sqrt {17} $.
Hướng dẫn giải:
- Vẽ $\overrightarrow {AB'} = 4\overrightarrow {AB} ;\,\,\,\,\,\,\overrightarrow {AC'} = - \overrightarrow {AC} $ sử dụng định nghĩa tích của một véc tơ với một số.
- Tìm véc tơ tổng \(\overrightarrow {AB'} + \overrightarrow {AC'} \) và tính độ dài của nó.