Câu hỏi:
2 năm trước
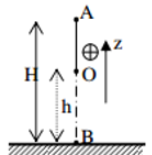
Tại điểm A cách mặt đất 5m một vật có khối lượng 4 kg được ném thẳng đứng lên trên với vận tốc đầu 10 m/s. Lấy g = 10 m/s2. Chọn mốc thế năng tại mặt đất. Bỏ qua lực cản không khí.Tốc độ của vật khi vật đi được quãng đường 7 m kể từ vị trí ném vật là:
Trả lời bởi giáo viên
Đáp án đúng: d
+ Cơ năng tại A:
\({{\rm{W}}_A} = \dfrac{1}{2}.m.{v^2} + m.g.z = \dfrac{1}{2}{.4.10^2} + 4.10.5 = 400\left( J \right)\)
Gọi vị trí cao nhất mà vật có thể đạt được là D. Gọi C là vị trí vật đi được 7m kể từ vị trí ném.
+ Cơ năng tại D: \({W_D} = m.g.{z_D}\)
Áp dụng bảo toàn cơ năng cho A và D ta có:
\({{\rm{W}}_A} = {{\rm{W}}_D} \Rightarrow 400 = m.g.{z_D} \Rightarrow {z_D} = 10m\)
Vậy độ cao cực đại vật có thể đạt được là : \({h_{max}} = 10m\)
Vậy khi đi lên từ A đến D, vật đi được quãng đường 5m; sau đó rơi xuống 2m thì vật sẽ đi được quãng đường 7m.
Vậy tọa độ của điểm C là: \({z_C} = 8m\)
Áp dụng bảo toàn cơ năng cho A và C ta có:
\(\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_C} = 400J \Rightarrow 400 = m.g.{z_C} + \dfrac{1}{2}.m.v_C^2\\ \Rightarrow 400 = 4.10.8 + \dfrac{1}{2}.4.v_C^2 \Rightarrow {v_C} = 2\sqrt {10} \left( {m/s} \right)\end{array}\)
Hướng dẫn giải:
Công thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}.m.{v^2}\)
Công thức tính thế năng : \({W_t} = m.g.z\)
Công thức tính cơ năng: \({\rm{W}} = \dfrac{1}{2}.m.{v^2} + m.g.z\)
Áp dụng định luật bảo toàn cơ năng: \({W_A} = {W_C} = {{\rm{W}}_D}\)
