Trả lời bởi giáo viên
Đáp án đúng: c
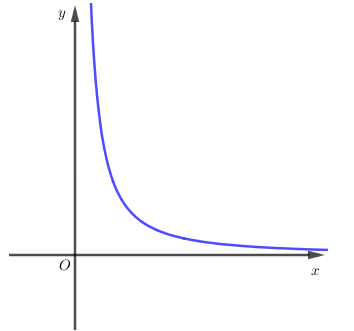
Đồ thị hàm số có $2$ đường tiệm cận là
- Tiệm cận đứng $x = 2$
- Tiệm cận ngang $y = - 1$
Hướng dẫn giải:
$x = {x_o}$ là tiệm cận đứng của đồ thị hàm số $y = f\left( x \right)$ nếu: $\left[ \begin{gathered} \mathop {\lim }\limits_{x \to x_o^ - } \,f\left( x \right) = + \infty \hfill \\ \mathop {\lim }\limits_{x \to x_o^ - } f\left( x \right) = - \infty \hfill \\ \mathop {\lim }\limits_{x \to x_o^ + } f\left( x \right) = + \infty \hfill \\ \mathop {\lim }\limits_{x \to x_o^ + } \,f\left( x \right) = - \infty \hfill \\ \end{gathered} \right.$
$y = {y_o}$ là tiệm cận ngang của đồ thị hàm số $y = f\left( x \right)$ nếu $\left[ \begin{gathered} \mathop {\lim }\limits_{x \to + \infty } \,f\left( x \right) = {y_o} \hfill \\ \mathop {\lim }\limits_{x \to - \infty } \,f\left( x \right) = {y_o} \hfill \\ \end{gathered} \right.$
Giải thích thêm:
Có thể kết luận nhanh bằng cách áp dụng tính chất hàm phân thức $y = \dfrac{{ax + b}}{{cx + d}}\left( {ac \ne bd} \right)$ sẽ có hai tiệm cận $x = - \dfrac{d}{c};y = \dfrac{a}{c}$.
