Câu hỏi:
3 năm trước
Số điểm cực đại của hàm số \(y = \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)...\left( {x - 100} \right)\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
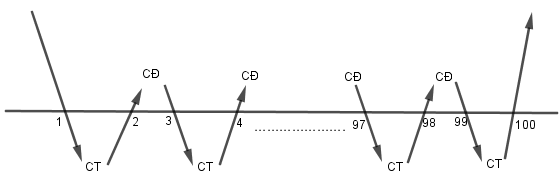
Xét phương trình \(y = \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)...\left( {x - 100} \right) = 0\), phương trình có 100 nghiệm phân biệt.
Phương trình \(y = f\left( x \right) = 0\) là phương trình bậc 100, có 100 nghiệm, do đó hàm số \(y = f\left( x \right)\) có 99 điểm cực trị.
Lại có \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên số điểm cực tiểu nhiều hơn số điểm cực đại là 1.
Do đó hàm số có 50 điểm cực tiểu, 49 điểm cực đại.


