Câu hỏi:
3 năm trước
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(C,\)\(AB = a\sqrt 5 ,\)\(AC = a.\) Cạnh bên \(SA = 3a\) và vuông góc với mặt phẳng đáy. Thể tích của khối chóp \(S.ABC\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
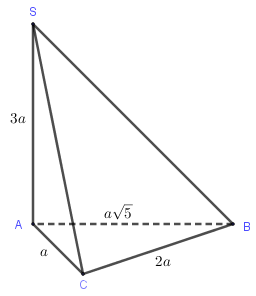
Vì \(\Delta ABC\) vuông nên áp dụng pitago.
\(CB = \sqrt {A{B^2} - A{C^2}} = \sqrt {5{a^2} - {a^2}} = 2a.\).
Diện tích đáy \({S_{\Delta ABC}} = \dfrac{1}{2}.a.2a = {a^2}\).
Thể tích khối chóp: \({V_{S.ABC}} = \dfrac{1}{3}.{S_{\Delta ABC}}.SA = \dfrac{1}{3}.{a^2}.3a = {a^3}.\)
Hướng dẫn giải:
Thể tích khối chóp \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.


