Ông \(A\) dự định sử dụng hết \(6,5{m^3}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

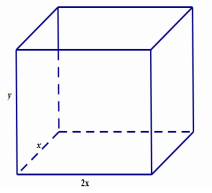
Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,2x,y\,\,\left( {x,y > 0} \right)\).

Diện tích phần lắp kính là:

\(\begin{array}{l}2x.x + 2xy + 2.2x.y = 2{x^2} + 6xy = 6,5\\ \Leftrightarrow xy = \frac{{6,5 - 2{x^2}}}{6} > 0 \Rightarrow x < \sqrt {\frac{{6,5}}{2}}  = \frac{{\sqrt {13} }}{2}.\end{array}\)

Thể tích bể cá là: \(V = 2x.x.y = 2x.\frac{{6,5 - 2{x^2}}}{6} = \frac{{ - 4{x^3} + 13x}}{6}\) với \(0 < x < \frac{{\sqrt {13} }}{2}\)

Ta có: \(V' = \frac{{ - 12{x^2} + 13}}{6},V' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{\sqrt {39} }}{6}\\x =  - \frac{{\sqrt {39} }}{6}\left( L \right)\end{array} \right.\)

Bảng biến thiên:

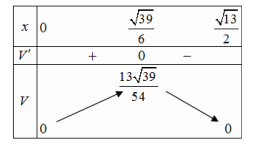
Vậy \({V_{\max }} = \frac{{13\sqrt {39} }}{{54}} \approx 1,50\,{m^3}\)