Cho hình chóp S.ABCD có đáy \({\rm{ABCD}}\) là hình bình hành. Gọi \(G\) là trọng tâm tam giác $A B C$ và \(M\) là trung điểm $S C$. Gọi \(K\) là giao điểm của $S D$ với mặt phẳng \((AGM)\). Tỉ số \(\dfrac{{KS}}{{KD}}\) bằng:

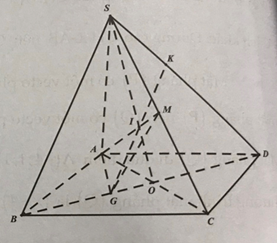
 Gọi \(O = AC \cap BD,I = AM \cap SO\).

Trong mặt phẳng \(({\rm{SBD}})\), kéo dài GI cắt \({\rm{SD}}\) tại \({\rm{K}}\) \( \Rightarrow K = SD \cap (AMG)\).

Trong tam giác \({\rm{SAC}}\), có \({\rm{SO}},{\rm{AM}}\) là hai đường trung tuyến. Suy ra I là trọng tâm tam giác SAC \( \Rightarrow \dfrac{{{\rm{OI}}}}{{{\rm{OS}}}} = \dfrac{1}{3}\) mà \(\dfrac{{{\rm{OG}}}}{{{\rm{OB}}}} = \dfrac{1}{3} \Rightarrow \dfrac{{{\rm{OI}}}}{{{\rm{OS}}}} = \dfrac{{{\rm{OG}}}}{{{\rm{OB}}}} \Rightarrow {\rm{GI}}//{\rm{SB}}\) \( \Rightarrow {\rm{GK}}//{\rm{SB}} \Rightarrow \dfrac{{{\rm{KD}}}}{{{\rm{KS}}}} = \dfrac{{{\rm{GD}}}}{{{\rm{GB}}}}\).

Ta có \({\rm{DO}} = {\rm{BO}} = 3{\rm{GO}} \Rightarrow {\rm{GD}} = 4{\rm{GO}},{\rm{GB}} = 2{\rm{GO}}\).

Vậy \(\dfrac{{{\rm{KD}}}}{{{\rm{KS}}}} = \dfrac{{{\rm{GD}}}}{{{\rm{GB}}}} = \dfrac{{4{\rm{GO}}}}{{2{\rm{GO}}}} = 2 \Rightarrow \dfrac{{{\rm{KS}}}}{{{\rm{KD}}}} = \dfrac{1}{2}\).