Ở mặt nước, tại hai điểm A và B có hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng. ABCD là hình vuông nằm ngang. Biết trên CD có 3 vị trí mà ở đó các phần tử dao động với biên độ cực đại. Trên AB có tối đa bao nhiêu vị trí mà phần tử ở đó dao động với biên độ cực đại?
Trả lời bởi giáo viên
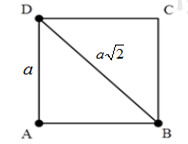
Gọi a là độ dài cạnh hình vuông ABCD.
Áp dụng định lí Pitago ta có :
\(BD = \sqrt {A{D^2} + A{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Trên CD có 3 vị trí 3 vị trí mà ở đó các phần tử dao động với biên độ cực đại nên :
\(BD - AD \le 2\lambda \Leftrightarrow a\sqrt 2 - a \le 2\lambda \Rightarrow \lambda \ge \dfrac{{a\sqrt 2 - a}}{2}\)
Ta xét tỉ số :
\(\dfrac{{AB}}{\lambda } = \dfrac{a}{\lambda } \le \dfrac{a}{{\dfrac{{a\sqrt 2 - a}}{2}}} \Leftrightarrow \dfrac{{AB}}{\lambda } \le 4,8\)
Vậy : \( - 4,8 \le k \le 4,8 \Rightarrow k = - 4; - 3;...;4\)
Vậy trên AB có tối đa 9 cực đại.
Hướng dẫn giải:
Điều kiện có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha : \({d_2} - {d_1} = k\lambda \)
Số cực đại giao thoa trên đoạn AB bằng số giá trị k nguyên thoả mãn : \( - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda }\)

