Một vật khối lượng \(m = 1kg\) trượt từ đỉnh của mặt phẳng nghiêng cao \(1m\), dài \(10m\). Lấy \(g = 9,8m/{s^2}\), hệ số ma sát là \(0,05\)

Tính quãng đường mà vật đi thêm được cho đến khi dừng hẳn trên mặt phẳng ngang?

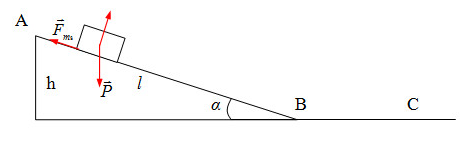
Ta có:

+ Cơ năng tại A: \({{\rm{W}}_A} = mgh = 1.9,8.1 = 9,8J\)

+ Trong khi vật chuyển động từ A đến B, tại B cơ năng chuyển hóa thành động năng tại B và công để thắng lực ma sát

Áp dụng định luật bảo toàn chuyển hóa năng lượng, ta có:

\({{\rm{W}}_A} = {{\rm{W}}_{{d_B}}} + {A_{{F_{ms}}}}\)  (1)

Chọn chiều dương trùng chiều chuyển động của vật

Ta có:

+ Động năng tại B: \({{\rm{W}}_{{d_B}}} = \dfrac{1}{2}mv_B^2\)

+ Công của lực ma sát: \(A = {F_{ms}}.s.cos\beta  =  - {F_{ms}}.l =  - \mu P.\sin \alpha .l\)

Thay vào (1) ta được:

\(\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_{{d_B}}} + \left| {{A_{{F_{ms}}}}} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}mv_B^2 + \left| { - \mu .P.\sin \alpha .l} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}m.v_B^2 + \left| { - \mu mg.\dfrac{h}{l}.l} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}1.v_B^2 + \left| { - 0,05.1.9,8.\dfrac{1}{{10}}.10} \right|\\ \to v_B^2 = 18,62\\ \to {v_B} \approx 4,32m/s\end{array}\)

+ Tại điểm C, vật dừng lại

=> Toàn bộ động năng tại B đã chuyển thành năng lượng để thắng lực ma sát trên đoạn BC

Ta có:

\(\begin{array}{l}{{\rm{W}}_{{d_B}}} = \left| {{A_{BC}}} \right| = \mu mg.BC\\ \leftrightarrow \dfrac{1}{2}mv_B^2 = \mu mg.BC\\ \leftrightarrow \dfrac{1}{2}.1.4,{32^2} = 0,05.1.9,8.BC\\ \to BC = 19m\end{array}\)