Một vật dao động điều hòa với phương trình \(x = 6cos\left( {20\pi t + \dfrac{\pi }{6}} \right)cm\). Tốc độ trung bình của vật đi từ vị trí cân bằng theo chiều dương đến vị trí có li độ \(x = 3cm\) theo chiều dương là:
Trả lời bởi giáo viên
+ Chu kì dao động của vật: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{20\pi }} = 0,1s\)
+ Khi vật đi từ vị trí cân bằng theo chiều dương đến vị trí $x = 3 cm$ theo chiều dương
+ Quãng đường đi được: $S = 3cm$
+ Thời gian đi (sử dụng vòng tròn lượng giác)
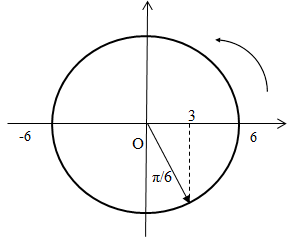
Góc quét được: \(\dfrac{\pi }{6}\)
=> Thời gian vật đi từ vị trí cân bằng theo chiều dương đến vị trí \(x = 3cm\) theo chiều dương là: \(\Delta t = \dfrac{T}{{12}} = \dfrac{1}{{120}}s\)
=> Tốc độ trung bình: \({v_{tb}} = \dfrac{S}{{\Delta t}} = \dfrac{{3cm}}{{\dfrac{1}{{120}}}} = 360cm/s = 3,6m/s\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính chu kì: \(T = \dfrac{{2\pi }}{\omega }\)
+ Sử dụng vòng tròn lượng giác và biểu thức: \(\Delta \varphi = \omega \Delta t\)
+ Tốc độ trung bình: \({v_{tb}} = \dfrac{S}{{\Delta t}}\) (S là quãng đường vật đi được trong thời gian \(\Delta t\))

