Một vật dao động điều hòa trên trục Ox với phương trình \(x = 10\cos \left( {4\pi t + \dfrac{{2\pi }}{3}} \right)cm\) (t tính bằng s). Thời điểm đầu tiên kể từ \(t = 0\) vận tốc của vật đạt giá trị cực đại là
Trả lời bởi giáo viên
Chu kì dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\)
Vận tốc của vật đạt giá trị cực đại khi vật qua VTCB qua chiều dương.
Biểu diễn trên VTLG ta có:
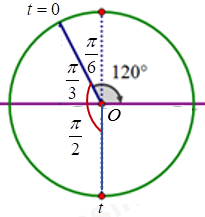
Góc quét tương ứng: \(\alpha = \dfrac{\pi }{3} + \dfrac{\pi }{2} = \dfrac{{5\pi }}{6}\)
\( \Rightarrow \Delta t = \alpha .\dfrac{T}{{2\pi }} = \dfrac{{5\pi }}{6}.\dfrac{T}{{2\pi }} = \dfrac{{5T}}{{12}} = \dfrac{{5.0,5}}{{12}} = \dfrac{5}{{24}}s\)
Hướng dẫn giải:
Vận tốc của vật đạt giá trị cực đại khi vật qua VTCB qua chiều dương.
Sử dụng VTLG và công thức tính góc quét \(\alpha = \omega .\Delta t\)

 (Nguồn: ourwordindata.org)
(Nguồn: ourwordindata.org)